pwn入门-整数溢出

原理

整数溢出”漏洞，是计算机在对数值处理(存储、运算、条件判断)过程中，产生了不符合预期理论设计的错误，使得计算机本身行为偏离预期(漏洞)。

譬如，预期的理论设计是1+1=2，但由于不可知的错误(发生在存储、运算时)，导致了1+1=3，程序(软件层面)还依赖于3这个数值(条件判断、运算)，那么计算机的行为，就会偏离预期了。

存储角度

计算机存储一个“整数”，是“模2的偶数次幂”的原理。负数的编码上，也只是一个移码，它只是把整个“负数集合”，从左往右挪(移)，假设左边是负数，右边是整数。 至于补码，其实就是加了一个“轮回”(2的偶数次幂)。至于，浮点数的存储原理，和整数非常不同。

浮点数，主要是涉及一个“无论多少位都无法精确表达”的问题，就是IEEE754中，浮点数设计的缺陷。在十进制中，唯有尾数是0或5的小数，才可以理论上被精确表示。

浮点数，用一个三元组表示 {Sign, Exponent, Significance}。其中，指数位(Exponent)，主要是一个移码的设计。当指数位为全0的时候，可以表示十进制数0。当指数位全1的时候，可以表示正/负无穷。此上述两者为特殊数值，故去掉后，码位减少了2个位置。在减少两个位置的情况下，将正数、负数，“均等”地编码在这些码位上，则移码的偏移量为127。如果指数是3，则机器存储，为3+127=130；负数同理，亦是加上127，再进行机器存储。这个移码设计，保证了存储上，正数大于负数。

运算角度

如果连浮点数都能轻易理解，那么理解整数，整数上的模2群运算，应该不成问题。顶多涉及一些编码(负数挪位置)的问题。

显然，一个数(无符号数)，加着加着，或者减着减着，或者去做乘法，它有可能溢出，跑到负数的编码位置上。如果程序设计不好，将这个“不符合预期理论设计”得出的数，当作一个有符号数(负数)进行处理，那肯定出问题。

条件判断角度

这个涉及X86的汇编，就是OF标志位和SF标志位。OF标志位，只对无符号数有意义，因为，正数加正数，不会出现一个负数(符号位为1)；负数加负数，不会出现一个正数(符号位为0)。

至于，SF，就更简单了，记录了运算结果的符号位。SF，运算结果是正数，就是0；运算结果是负数，就是1。X86的计算机，根据这两个标志位，就可以进行有符号数、无符号数的大小判断了。

现实(In practice)

现实中，上面三个，导致“整数溢出”漏洞的诱因，往往综合起来出现。

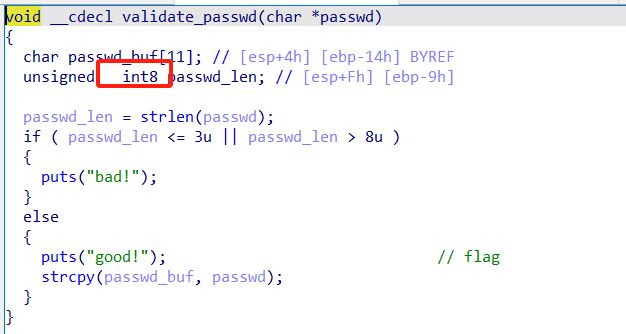
举个例子，譬如，体现在一个函数(功能)上：有一个函数(如atoi、strlen函数等)，对输入的字符进行处理，并转化为数值。如果该数值，存储的过程中，被模，“截断了”，那么它导致程序出现非预期行为的概率非常大。如果，后续，还用这个数值做判断，那不就是多个诱因综合出现嘛。

靠人

因为，“整数溢出”漏洞，是跟“预期理想设计”相关的。 说白了，就像是人，在做(软件)工程质检：你的预期设计是这样的，但是工程上，这样子处理这些数值，会使计算机出现非预期的行为。那就需要，那个“人”，质检员，对“整数溢出”漏洞，有深入的理解，一定的实践经验。

靠机器、方法论

如何定义，什么是“预期设计”，什么是“非预期设计”，是个难点。