TSCTF-J 2024

iPlayIDA

直接解码发现不对，函数很少，查看其它函数发现隐藏逻辑在初始化里

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import base64
enc = 'kzMrkZiFDGFLeSz9b4uCL/xPLu1EfVkNQ4kmk46NqwxYmx=='

key = [  0x72,0x1A,0x73,0x36,0x1F,0x3C,0x15,0x31,
  0x78,0x3E,0x3D,0x05,0x3C,0x03,0x7D,0x3E,
  0x29,0x35,0x17,0x07,0x3A,0x3D,0x20,0x14,
  0x30,0x3F,0x2E,0x00,0x32,0x02,0x2E,0x0B,
  0x06,0x31,0x0A,0x53,0x03,0x2F,0x3B,0x29,
  0x2E,0x3A,0x49,0x16,0x03,0x32,0x37,0x5D,
  0x27,0x4F,0x37,0x3F,0x65,0x44,0x06,0x1C,
  0x58,0x00,0x61,0x63,0x70,0x0F,0x41,0x5C]

table = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/'

strflag = [chr(ord(table[i]) ^ key[i]) for i in range(len(table))]

new_table = ''.join([i for i in strflag])
def base64decode(s):
    old_table = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/'
    new_table = '3X0rZzRy1tvIqM2nxgDSokwLieObQfKmaYc9hCVGAJ8dpFB+P7NEUu4/l5WTH6js'
    s = s.translate(str.maketrans(new_table, old_table))
    return base64.b64decode(s)

print(base64decode('kzMrkZiFDGFLeSz9b4uCL/xPLu1EfVkNQ4kmk46NqwxYmx=='))

TSCTF-J{We1come_t0_R3verse_Wor1d!}

iPlayPython

pyinstxtractor.py 解python包

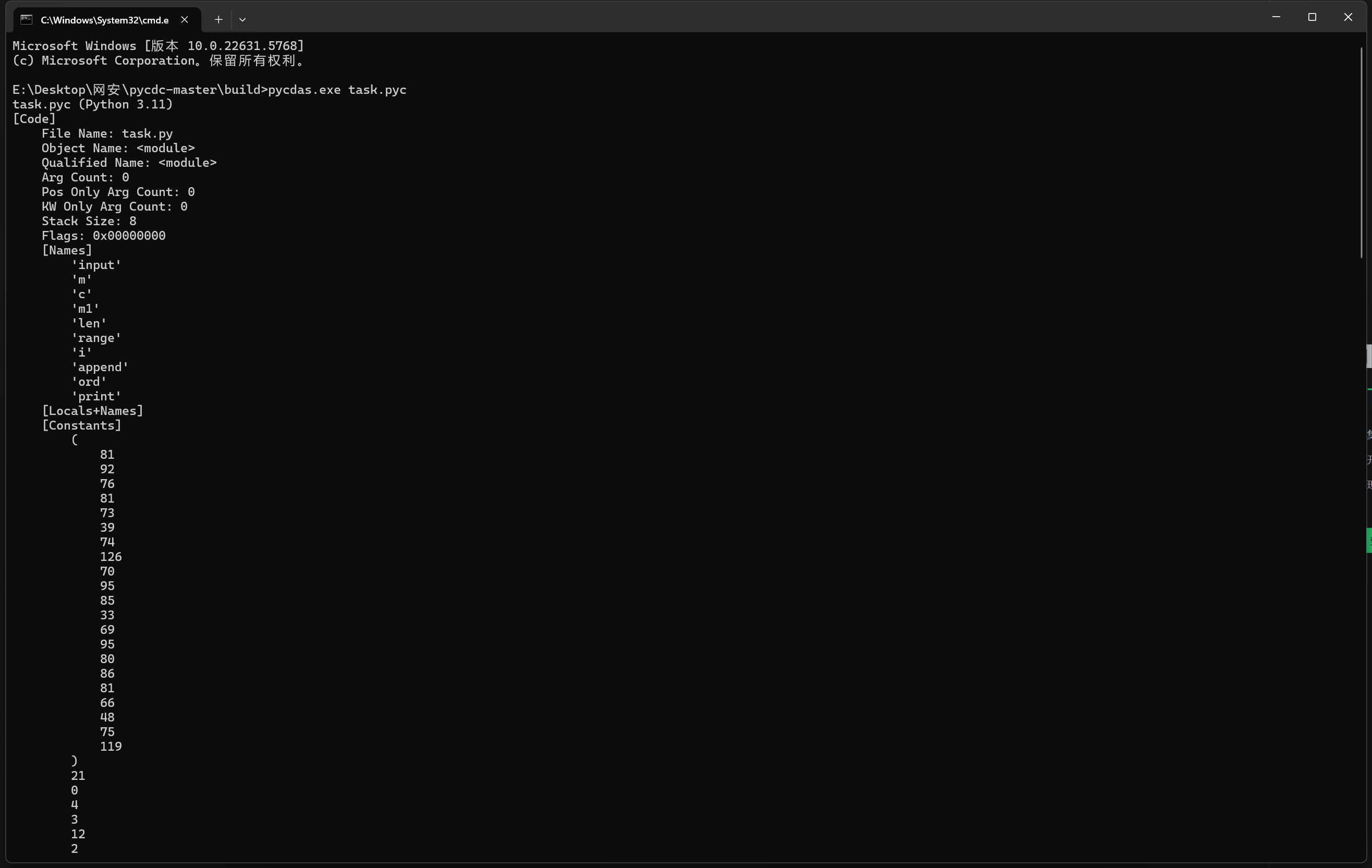
反编译pyc文件出现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#!/usr/bin/env python
# visit https://tool.lu/pyc/ for more information
# Version: Python 3.11

m = input()
c = [
    81,
    92,
    76,
    81,
    73,
    39,
    74,
    126,
    70,
    95,
    85,
    33,
    69,
    95,
    80,
    86,
    81,
    66,
    48,
    75,
    119]
m1 = []
# WARNING: Decompyle incomplete

这是模仿的一道NewStarCTF的一道题

用网上下的不行会出现Magic错误

我自己用源码编译了一份

image-20250910184907955

image-20250910185045148

可以看出来有某些移位操作

1
2
3
4
5
6
7
8
9
10
11
12
13
# 解题脚本：根据题目字节表 c 逆向还原原始输入
# 变换 T(x) = (x & 0xF0) | ((x & 0x0C) >> 2) | ((x & 0x03) << 2)，且 T 为自反（应用两次还原）

c = [81, 92, 76, 81, 73, 39, 74, 126, 70, 95, 85, 33, 69, 95, 80, 86, 81, 66, 48, 75, 119]

def T(x: int) -> int:
    return (x & 0xF0) | ((x & 0x0C) >> 2) | ((x & 0x03) << 2)

flag = ''.join(chr(T(x)) for x in c)
print(flag)

# 可选校验：再次应用 T 应等于原 c
assert [T(ord(ch)) for ch in flag] == c

TSCTF-J{I_U$E_PYTH0N}

可以看

NewStar PangBai 过家家（3） | Matriy’s blog和pycdc工具编译使用(纯小白篇，大师傅自动略过) - 吾爱破解 - 52pojie.cn

iPlayPinball

没啥头绪一开始，查了下

对于一般的文件结构，都会有一个后缀为_Data的文件夹，并且里面有一个名为Managed的文件夹，而那个文件夹里的Assembly-CSharp.dll文件正是我们需要的东西，里面包含了作者的代码

image-20250910193400789

发现相应逻辑

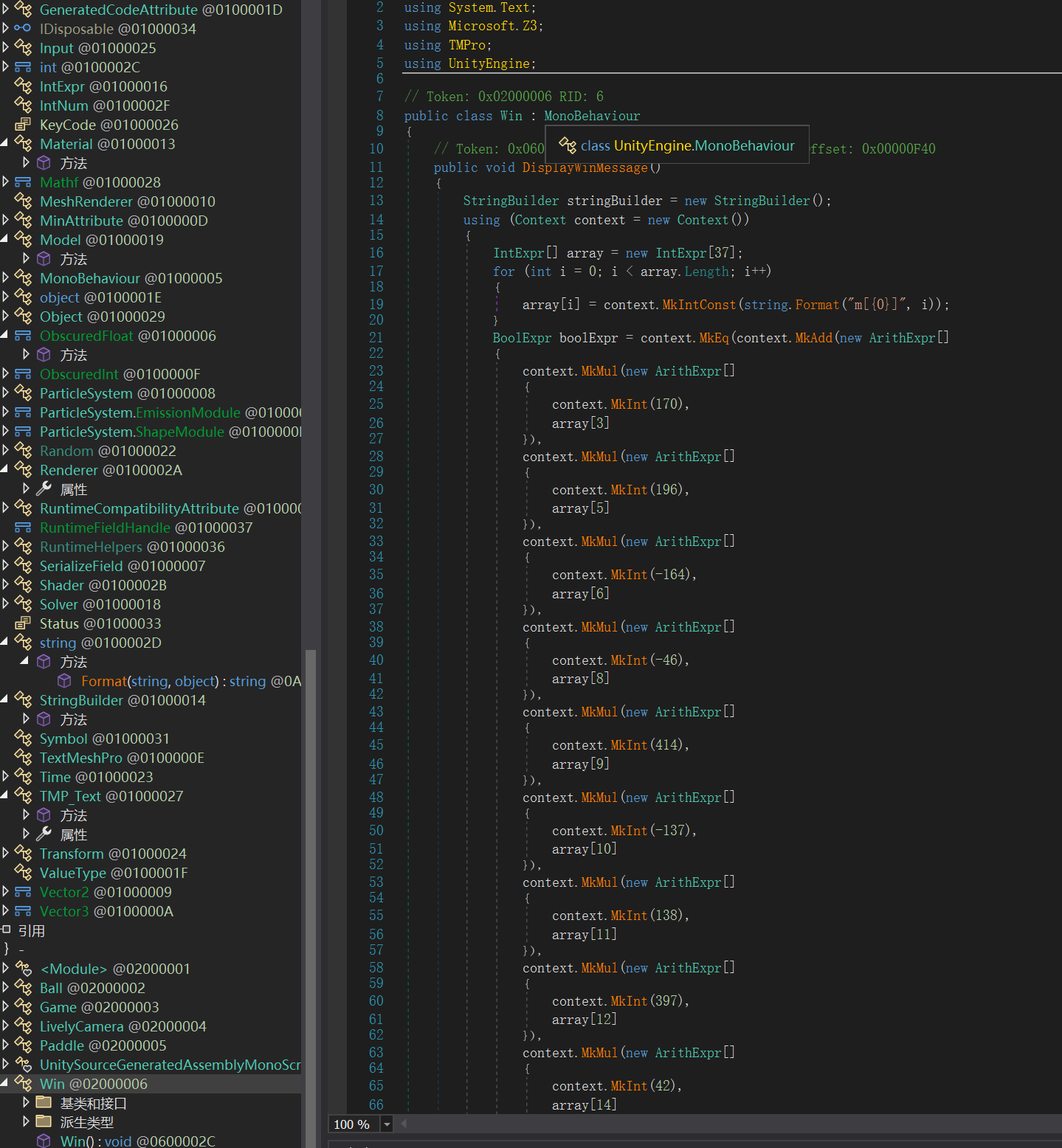
通过分析 question.txt 中的代码，我发现这是一个使用Microsoft Z3约束求解器的Unity游戏。主要逻辑在 Win 类的 DisplayWinMessage 方法中：

  1. 创建了一个长度为37的整数数组 array ，每个元素都是Z3的整数变量
  2. 定义了37个布尔表达式（方程），每个表达式都是一个线性方程，形式为：系数1×变量1 + 系数2×变量2 + … = 常数
  3. 将所有方程组合成一个大的约束条件
  4. 使用Z3求解器求解这个约束系统
  5. 如果有解，将解转换为字符，拼接成字符串显示为胜利信息（即flag）

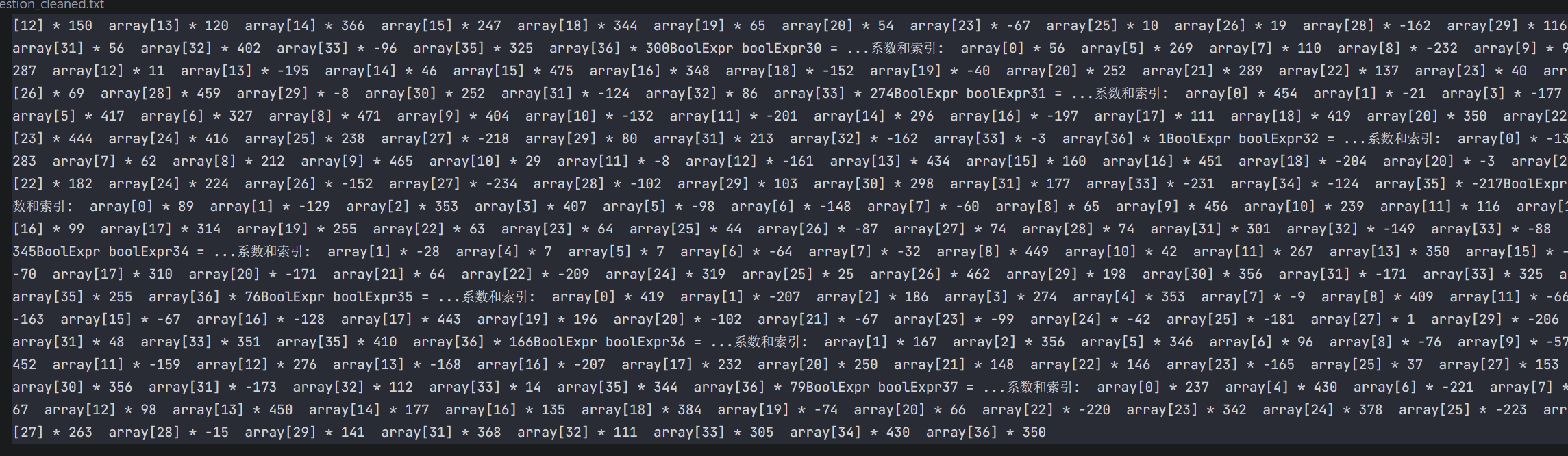
手动复制太麻烦可以写代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
import re

def clean_file(input_path, output_path):
    # 读取原始文件
    with open(input_path, 'r', encoding='utf-8') as f:
        lines = f.readlines()
    
    # 提取有用的信息
    cleaned_lines = []
    i = 0
    while i < len(lines):
        line = lines[i].strip()
        
        # 如果找到方程定义的开始
        if 'BoolExpr boolExpr' in line or re.match(r'BoolExpr boolExpr\d+', line):
            equation_name = line.split('=')[0].strip()
            cleaned_lines.append(f"{equation_name} = ...")
            
            # 收集方程中的系数和索引
            coefficients = []
            j = i + 1
            while j < len(lines) and '));' not in lines[j]:
                coef_match = re.search(r'context\.MkInt\(([-]?\d+)\)', lines[j])
                array_match = re.search(r'array\[(\d+)\]', lines[j+1] if j+1 < len(lines) else '')
                
                if coef_match and array_match:
                    coef = coef_match.group(1)
                    idx = array_match.group(1)
                    coefficients.append(f"array[{idx}] * {coef}")
                
                j += 1
                
            # 添加系数和索引信息
            if coefficients:
                cleaned_lines.append("系数和索引:")
                for coef_info in coefficients:
                    cleaned_lines.append(f"  {coef_info}")
            
            # 找到最后一个常数值
            while i < len(lines):
                if 'context.MkInt(' in lines[i] and '));' in lines[i+1:i+5]:
                    constant_match = re.search(r'context\.MkInt\((\d+)\)', lines[i])
                    if constant_match:
                        constant = constant_match.group(1)
                        cleaned_lines.append(f"常数值: {constant}\n")
                if '));' in lines[i]:
                    break
                i += 1
        
        # 保留其他重要信息
        elif 'array[' in line and not ('context.MkMul' in line or 'context.MkInt' in line):
            cleaned_lines.append(line + '\n')
        elif 'BoolExpr boolExpr38 = context.MkAnd' in line:
            cleaned_lines.append("\n合并所有方程:\n" + line + '\n')
        elif 'Solver solver = context.MkSolver()' in line:
            cleaned_lines.append("\n求解器部分:\n" + line + '\n')
        elif 'if (solver.Check() == Status.SATISFIABLE)' in line:
            cleaned_lines.append(line + '\n')
        elif 'Model model = solver.Model' in line:
            cleaned_lines.append(line + '\n')
        elif 'string text = ""' in line or 'for (int i = 0; i < 37; i++)' in line:
            cleaned_lines.append(line + '\n')
        
        i += 1
    
    # 写入新文件
    with open(output_path, 'w', encoding='utf-8') as f:
        f.writelines(cleaned_lines)
    
    print(f"处理完成，结果已保存到 {output_path}")

# 执行清理
input_file = "e:\\Desktop\\TSCTF\\t3\\Pinball\\question.txt"
output_file = "e:\\Desktop\\TSCTF\\t3\\Pinball\\question_cleaned.txt"
clean_file(input_file, output_file)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import re

def extract_constants(input_path, output_path):
    # 读取原始文件
    with open(input_path, 'r', encoding='utf-8') as f:
        content = f.read()
    
    # 使用正则表达式提取所有方程和对应的常数值
    pattern = r'BoolExpr boolExpr(\d*?)\s*=\s*context\.MkEq\([\s\S]+?context\.MkInt\((\d+)\)\);'
    matches = re.findall(pattern, content)
    
    # 将结果写入输出文件
    with open(output_path, 'w', encoding='utf-8') as f:
        for match in matches:
            equation_num = match[0] if match[0] else ''
            constant = match[1]
            f.write(f"boolExpr{equation_num}: {constant}\n")

if __name__ == "__main__":
    input_path = "question.txt"
    output_path = "constants.txt"
    extract_constants(input_path, output_path)

效果如下：

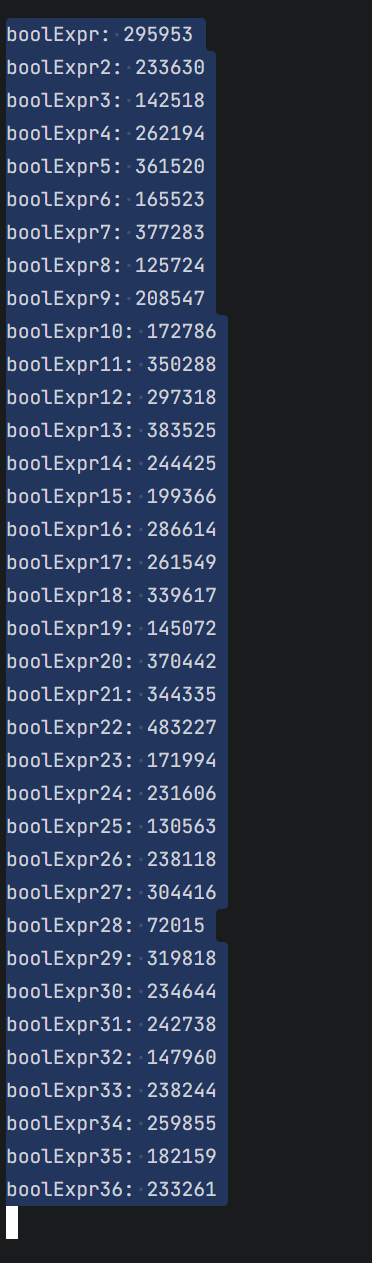
image-20250910202451587

image-20250910202513199

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
from z3 import *

# 创建Z3求解器和变量
solver = Solver()
array = [Int(f'array_{i}') for i in range(37)]

# 添加约束条件（从question_cleaned.txt中提取的方程）
# boolExpr
solver.add(170*array[3] + 196*array[5] + (-164)*array[6] + (-46)*array[8] + 414*array[9] +
          (-137)*array[10] + 138*array[11] + 397*array[12] + 42*array[14] + (-9)*array[15] +
          (-122)*array[16] + 459*array[18] + 427*array[19] + 418*array[20] + 176*array[21] +
          (-143)*array[22] + 281*array[24] + 202*array[25] + 419*array[26] + 262*array[27] +
          (-15)*array[28] + (-107)*array[30] + 358*array[31] + (-101)*array[32] + (-194)*array[33] == 295953)

# boolExpr2
solver.add(305*array[0] + 147*array[1] + 262*array[2] + (-68)*array[3] + 392*array[6] +
          214*array[7] + 251*array[8] + (-43)*array[9] + 85*array[10] + 8*array[12] +
          132*array[15] + (-197)*array[19] + 262*array[20] + (-153)*array[21] + (-192)*array[22] +
          (-222)*array[24] + 467*array[26] + (-152)*array[28] + 176*array[29] + 5*array[30] +
          237*array[31] + (-131)*array[32] + (-72)*array[33] + 187*array[34] + 477*array[36] == 233630)

# boolExpr3
solver.add(193*array[0] + 224*array[2] + (-57)*array[3] + 201*array[7] + (-140)*array[8] +
          448*array[9] + 98*array[10] + (-229)*array[13] + (-225)*array[16] + 0*array[17] +
          239*array[18] + (-186)*array[19] + 473*array[20] + 114*array[21] + 148*array[23] +
          (-147)*array[24] + 233*array[25] + 398*array[26] + (-114)*array[27] + (-153)*array[28] +
          (-225)*array[29] + (-199)*array[30] + 326*array[31] + 116*array[32] + 88*array[34] == 142518)

# boolExpr4
solver.add(170*array[0] + 224*array[1] + (-167)*array[3] + (-142)*array[4] + 183*array[5] +
          120*array[6] + (-97)*array[8] + 99*array[9] + 262*array[10] + 295*array[13] +
          111*array[14] + 35*array[15] + 219*array[18] + (-192)*array[19] + 230*array[21] +
          358*array[23] + 464*array[24] + 330*array[25] + (-157)*array[26] + 385*array[27] +
          246*array[31] + 135*array[32] + 194*array[33] + (-155)*array[35] + 73*array[36] == 262194)

# boolExpr5
solver.add(48*array[1] + 211*array[4] + 417*array[5] + 283*array[7] + (-198)*array[9] +
          404*array[10] + 274*array[11] + (-136)*array[12] + 97*array[13] + 333*array[14] +
          355*array[15] + 350*array[17] + 144*array[18] + (-45)*array[19] + 33*array[20] +
          458*array[21] + (-139)*array[22] + 169*array[23] + (-22)*array[24] + 239*array[27] +
          227*array[29] + 210*array[30] + 54*array[33] + 152*array[35] + 105*array[36] == 361520)

# boolExpr6
solver.add(1*array[0] + (-57)*array[3] + (-219)*array[4] + 113*array[6] + 234*array[7] +
          128*array[8] + 16*array[10] + (-231)*array[11] + 86*array[12] + (-126)*array[13] +
          118*array[14] + 4*array[15] + (-210)*array[17] + (-82)*array[18] + 427*array[19] +
          (-86)*array[20] + 310*array[22] + 197*array[23] + 24*array[25] + 230*array[27] +
          (-127)*array[28] + 214*array[31] + 162*array[33] + 330*array[34] + 140*array[36] == 165523)

# boolExpr7
solver.add(444*array[1] + 326*array[2] + 469*array[3] + 306*array[5] + 415*array[8] +
          (-56)*array[9] + (-112)*array[10] + (-217)*array[11] + (-166)*array[12] + 202*array[13] +
          182*array[15] + 150*array[16] + 232*array[17] + 96*array[18] + 323*array[19] +
          416*array[20] + 24*array[21] + 137*array[22] + 226*array[23] + (-173)*array[26] +
          265*array[27] + 445*array[28] + 225*array[32] + 100*array[33] + 269*array[36] == 377283)

# boolExpr8
solver.add(355*array[0] + 269*array[1] + (-36)*array[3] + (-195)*array[4] + 264*array[5] +
          (-17)*array[6] + (-30)*array[8] + (-222)*array[9] + 175*array[11] + 480*array[12] +
          (-237)*array[13] + (-231)*array[14] + 464*array[15] + (-137)*array[17] + 51*array[20] +
          271*array[23] + (-176)*array[24] + 3*array[26] + 101*array[27] + 449*array[30] +
          (-144)*array[31] + (-173)*array[32] + (-76)*array[34] + 172*array[35] + 288*array[36] == 125724)

# boolExpr9
solver.add((-133)*array[4] + 146*array[5] + (-38)*array[6] + 38*array[7] + (-224)*array[8] +
          111*array[9] + 268*array[10] + (-84)*array[11] + 354*array[13] + (-7)*array[14] +
          380*array[15] + (-50)*array[17] + 12*array[18] + 312*array[20] + 268*array[21] +
          5*array[22] + (-80)*array[24] + 133*array[27] + 433*array[28] + 73*array[30] +
          285*array[31] + (-54)*array[33] + 234*array[34] + 113*array[35] + (-34)*array[36] == 208547)

# boolExpr10
solver.add((-121)*array[3] + (-133)*array[6] + (-114)*array[8] + (-229)*array[9] + 203*array[11] +
          271*array[12] + 115*array[14] + 253*array[15] + (-96)*array[16] + (-137)*array[17] +
          177*array[18] + (-76)*array[19] + 183*array[20] + 195*array[21] + 248*array[22] +
          250*array[23] + (-2)*array[25] + 239*array[27] + (-40)*array[28] + 328*array[29] +
          111*array[31] + 8*array[32] + 449*array[33] + (-3)*array[34] + 74*array[36] == 172786)

# boolExpr11
solver.add(209*array[0] + 187*array[2] + 389*array[3] + 157*array[4] + 304*array[5] +
          376*array[7] + 190*array[8] + 425*array[9] + 287*array[10] + (-2)*array[11] +
          372*array[12] + (-53)*array[13] + 441*array[16] + (-172)*array[17] + (-218)*array[18] +
          214*array[21] + (-230)*array[24] + 207*array[25] + 216*array[26] + (-194)*array[27] +
          444*array[28] + 299*array[32] + (-53)*array[33] + (-206)*array[34] + 313*array[35] == 350288)

# boolExpr12
solver.add(411*array[1] + 337*array[2] + 303*array[3] + (-3)*array[5] + 35*array[6] +
          12*array[7] + (-23)*array[8] + 99*array[9] + 303*array[12] + 320*array[13] +
          (-9)*array[14] + 39*array[15] + 411*array[17] + 191*array[18] + (-84)*array[19] +
          (-164)*array[20] + 444*array[21] + 323*array[24] + 162*array[25] + (-127)*array[27] +
          266*array[29] + 109*array[32] + 363*array[33] + 310*array[34] + (-141)*array[36] == 297318)

# boolExpr13
solver.add(250*array[0] + 57*array[1] + 466*array[4] + 97*array[5] + 259*array[6] +
          25*array[7] + (-35)*array[9] + 192*array[10] + (-161)*array[13] + 202*array[14] +
          435*array[15] + 325*array[16] + 216*array[17] + 23*array[20] + 202*array[21] +
          78*array[22] + 364*array[23] + 465*array[24] + 424*array[25] + 74*array[29] +
          253*array[30] + 274*array[31] + (-65)*array[32] + 155*array[33] + (-195)*array[35] == 383525)

# boolExpr14
solver.add(406*array[0] + 462*array[3] + 274*array[4] + (-131)*array[8] + (-175)*array[9] +
          101*array[11] + 204*array[12] + 130*array[13] + 103*array[14] + 278*array[15] +
          264*array[17] + (-15)*array[18] + 347*array[19] + (-221)*array[22] + (-240)*array[24] +
          53*array[25] + 465*array[27] + 16*array[28] + (-211)*array[29] + (-127)*array[31] +
          396*array[32] + (-68)*array[33] + 129*array[34] + (-69)*array[35] + 281*array[36] == 244425)

# boolExpr15
solver.add(437*array[0] + (-161)*array[2] + 175*array[3] + 106*array[4] + 73*array[6] +
          225*array[8] + 147*array[9] + 73*array[12] + 364*array[14] + 292*array[16] +
          (-128)*array[17] + (-104)*array[18] + (-48)*array[19] + (-172)*array[20] + 203*array[21] +
          (-59)*array[22] + 183*array[23] + 447*array[24] + (-235)*array[25] + 338*array[27] +
          98*array[28] + (-130)*array[30] + (-29)*array[31] + (-24)*array[32] + 229*array[34] == 199366)

# boolExpr16
solver.add(458*array[0] + 358*array[1] + 182*array[3] + 476*array[4] + 336*array[5] +
          255*array[7] + (-68)*array[8] + (-183)*array[9] + 111*array[10] + 392*array[11] +
          306*array[12] + 2*array[14] + 286*array[20] + 113*array[21] + (-47)*array[22] +
          (-30)*array[23] + (-84)*array[24] + 174*array[25] + (-194)*array[26] + (-132)*array[27] +
          414*array[31] + 206*array[32] + (-69)*array[33] + (-144)*array[34] + (-38)*array[36] == 286614)

# boolExpr17
solver.add(95*array[0] + (-24)*array[1] + 390*array[4] + 89*array[5] + 139*array[9] +
          93*array[10] + (-35)*array[12] + 372*array[13] + 33*array[14] + (-152)*array[15] +
          243*array[16] + 258*array[17] + 383*array[21] + (-49)*array[22] + (-184)*array[23] +
          133*array[25] + (-159)*array[27] + 400*array[28] + 422*array[29] + (-240)*array[30] +
          476*array[31] + 167*array[32] + 157*array[34] + (-215)*array[35] + 29*array[36] == 261549)

# boolExpr18
solver.add(138*array[1] + 36*array[2] + (-162)*array[3] + (-160)*array[4] + 293*array[5] +
          412*array[6] + 242*array[8] + 470*array[9] + 149*array[12] + 235*array[14] +
          169*array[15] + 265*array[16] + 148*array[18] + 386*array[20] + 100*array[21] +
          (-175)*array[22] + 399*array[24] + 110*array[25] + 24*array[28] + (-186)*array[29] +
          (-55)*array[30] + 473*array[31] + 312*array[32] + 476*array[33] + 21*array[35] == 339617)

# boolExpr19
solver.add(360*array[1] + 178*array[2] + (-206)*array[3] + 38*array[4] + 97*array[5] +
          43*array[6] + (-150)*array[10] + (-209)*array[11] + 132*array[12] + (-21)*array[15] +
          46*array[16] + 23*array[17] + 22*array[18] + 454*array[19] + 360*array[20] +
          386*array[21] + (-113)*array[22] + (-214)*array[25] + 99*array[26] + 362*array[27] +
          (-52)*array[28] + 73*array[31] + 221*array[33] + (-154)*array[34] + (-116)*array[36] == 145072)

# boolExpr20
solver.add(444*array[0] + 279*array[1] + 328*array[2] + 43*array[3] + 25*array[4] +
          268*array[6] + 148*array[7] + 321*array[8] + 141*array[10] + (-195)*array[11] +
          (-195)*array[12] + 114*array[13] + 362*array[14] + 309*array[16] + 283*array[17] +
          6*array[19] + 128*array[21] + 335*array[23] + 110*array[24] + 422*array[25] +
          (-48)*array[26] + 240*array[28] + (-104)*array[31] + 350*array[32] + (-25)*array[33] == 370442)

# boolExpr21
solver.add(98*array[0] + (-227)*array[2] + 134*array[4] + 204*array[5] + (-49)*array[7] +
          (-111)*array[8] + (-21)*array[11] + 171*array[12] + 104*array[13] + (-76)*array[14] +
          453*array[16] + (-196)*array[17] + 285*array[19] + (-150)*array[20] + 255*array[21] +
          216*array[22] + (-59)*array[24] + (-146)*array[25] + 325*array[26] + 336*array[27] +
          313*array[28] + 433*array[30] + 437*array[32] + 476*array[34] + 447*array[35] == 344335)

# boolExpr22
solver.add(341*array[2] + 280*array[3] + 362*array[7] + (-205)*array[8] + 415*array[9] +
          338*array[10] + 121*array[11] + 386*array[14] + 289*array[15] + (-138)*array[16] +
          (-89)*array[18] + 231*array[19] + 475*array[21] + 143*array[23] + 100*array[25] +
          52*array[26] + 264*array[27] + 469*array[28] + 455*array[29] + (-191)*array[30] +
          357*array[32] + 385*array[33] + 47*array[34] + 166*array[35] + 313*array[36] == 483227)

# boolExpr23
solver.add((-104)*array[0] + (-184)*array[1] + 185*array[2] + 343*array[3] + 168*array[4] +
          389*array[5] + 457*array[6] + 393*array[8] + 33*array[9] + (-174)*array[11] +
          (-134)*array[13] + (-74)*array[16] + (-90)*array[17] + (-70)*array[20] + (-148)*array[22] +
          (-169)*array[23] + 248*array[25] + (-175)*array[26] + 426*array[27] + 97*array[28] +
          74*array[29] + (-220)*array[30] + 439*array[32] + 139*array[33] + 281*array[36] == 171994)

# boolExpr24
solver.add((-114)*array[1] + (-202)*array[2] + 397*array[3] + (-182)*array[4] + (-22)*array[6] +
          (-119)*array[8] + (-194)*array[9] + (-89)*array[11] + 13*array[12] + (-63)*array[13] +
          144*array[15] + 203*array[16] + (-223)*array[17] + 240*array[19] + 416*array[20] +
          (-225)*array[22] + 307*array[23] + 274*array[24] + 421*array[26] + 326*array[29] +
          471*array[30] + 95*array[31] + 108*array[32] + 94*array[34] + (-19)*array[36] == 231606)

# boolExpr25
solver.add((-107)*array[0] + 422*array[1] + (-218)*array[2] + (-98)*array[3] + 76*array[5] +
          (-184)*array[6] + 278*array[7] + 87*array[10] + 167*array[11] + 226*array[13] +
          91*array[14] + (-216)*array[16] + 238*array[17] + 98*array[19] + (-158)*array[20] +
          (-101)*array[21] + 324*array[22] + 146*array[23] + (-73)*array[27] + 432*array[30] +
          89*array[32] + (-169)*array[33] + 105*array[34] + 115*array[35] + (-173)*array[36] == 130563)

# boolExpr26
solver.add(107*array[0] + 103*array[1] + 345*array[2] + 361*array[4] + (-101)*array[5] +
          94*array[7] + (-18)*array[8] + 255*array[9] + 144*array[11] + (-212)*array[12] +
          (-81)*array[13] + 436*array[15] + 184*array[16] + 118*array[19] + 423*array[20] +
          (-175)*array[22] + 4*array[25] + 275*array[27] + 441*array[28] + (-16)*array[29] +
          (-61)*array[30] + 198*array[31] + (-149)*array[32] + 24*array[33] + 81*array[36] == 238118)

# boolExpr27
solver.add(139*array[0] + (-135)*array[1] + 369*array[2] + 59*array[3] + (-205)*array[4] +
          344*array[5] + 292*array[6] + 262*array[7] + 396*array[10] + 467*array[13] +
          70*array[14] + (-177)*array[16] + (-162)*array[18] + 279*array[19] + 47*array[20] +
          171*array[21] + 190*array[22] + (-117)*array[23] + 256*array[24] + 329*array[26] +
          333*array[27] + 10*array[29] + 299*array[31] + 55*array[33] + (-167)*array[36] == 304416)

# boolExpr28
solver.add(172*array[0] + 35*array[2] + 89*array[5] + (-216)*array[6] + (-36)*array[7] +
          449*array[9] + 383*array[11] + (-5)*array[12] + 114*array[14] + (-121)*array[15] +
          (-98)*array[16] + 151*array[18] + (-23)*array[19] + (-233)*array[21] + 350*array[22] +
          (-33)*array[24] + (-188)*array[25] + (-148)*array[26] + 426*array[27] + 133*array[29] +
          (-219)*array[30] + 279*array[31] + (-169)*array[32] + (-32)*array[34] + 21*array[36] == 72015)

# boolExpr29
solver.add(415*array[1] + 304*array[2] + 314*array[4] + (-143)*array[6] + 182*array[7] +
          (-52)*array[8] + (-39)*array[10] + 150*array[12] + 120*array[13] + 366*array[14] +
          247*array[15] + 344*array[18] + 65*array[19] + 54*array[20] + (-67)*array[23] +
          10*array[25] + 19*array[26] + (-162)*array[28] + 116*array[29] + 259*array[30] +
          56*array[31] + 402*array[32] + (-96)*array[33] + 325*array[35] + 300*array[36] == 319818)

# boolExpr30
solver.add(56*array[0] + 269*array[5] + 110*array[7] + (-232)*array[8] + 91*array[9] +
          287*array[11] + 11*array[12] + (-195)*array[13] + 46*array[14] + 475*array[15] +
          348*array[16] + (-152)*array[18] + (-40)*array[19] + 252*array[20] + 289*array[21] +
          137*array[22] + 40*array[23] + (-46)*array[25] + 69*array[26] + 459*array[28] +
          (-8)*array[29] + 252*array[30] + (-124)*array[31] + 86*array[32] + 274*array[33] == 234644)

# boolExpr31
solver.add(454*array[0] + (-21)*array[1] + (-177)*array[3] + 5*array[4] + 417*array[5] +
          327*array[6] + 471*array[8] + 404*array[9] + (-132)*array[10] + (-201)*array[11] +
          296*array[14] + (-197)*array[16] + 111*array[17] + 419*array[18] + 350*array[20] +
          (-171)*array[22] + 444*array[23] + 416*array[24] + 238*array[25] + (-218)*array[27] +
          80*array[29] + 213*array[31] + (-162)*array[32] + (-3)*array[33] + 1*array[36] == 242738)

# boolExpr32
solver.add((-132)*array[0] + 283*array[1] + 62*array[7] + 212*array[8] + 465*array[9] +
          29*array[10] + (-8)*array[11] + (-161)*array[12] + 434*array[13] + 160*array[15] +
          451*array[16] + (-204)*array[18] + (-3)*array[20] + 216*array[21] + 182*array[22] +
          224*array[24] + (-152)*array[26] + (-234)*array[27] + (-102)*array[28] + 103*array[29] +
          298*array[30] + 177*array[31] + (-231)*array[33] + (-124)*array[34] + (-217)*array[35] == 147960)

# boolExpr33
solver.add(89*array[0] + (-129)*array[1] + 353*array[2] + 407*array[3] + (-98)*array[5] +
          (-148)*array[6] + (-60)*array[7] + 65*array[8] + 456*array[9] + 239*array[10] +
          116*array[11] + 57*array[14] + 99*array[16] + 314*array[17] + 255*array[19] +
          63*array[22] + 64*array[23] + 44*array[25] + (-87)*array[26] + 74*array[27] +
          74*array[28] + 301*array[31] + (-149)*array[32] + (-88)*array[33] + 345*array[35] == 238244)

# boolExpr34
solver.add((-28)*array[1] + 7*array[4] + 7*array[5] + (-64)*array[6] + (-32)*array[7] +
          449*array[8] + 42*array[10] + 267*array[11] + 350*array[13] + (-131)*array[15] +
          (-70)*array[16] + 310*array[17] + (-171)*array[20] + 64*array[21] + (-209)*array[22] +
          319*array[24] + 25*array[25] + 462*array[26] + 198*array[29] + 356*array[30] +
          (-171)*array[31] + 325*array[33] + 330*array[34] + 255*array[35] + 76*array[36] == 259855)

# boolExpr35
solver.add(419*array[0] + (-207)*array[1] + 186*array[2] + 274*array[3] + 353*array[4] +
          (-9)*array[7] + 409*array[8] + (-66)*array[11] + (-163)*array[14] + (-67)*array[15] +
          (-128)*array[16] + 443*array[17] + 196*array[19] + (-102)*array[20] + (-67)*array[21] +
          (-99)*array[23] + (-42)*array[24] + (-181)*array[25] + 1*array[27] + (-206)*array[29] +
          330*array[30] + 48*array[31] + 351*array[33] + 410*array[35] + 166*array[36] == 182159)

# boolExpr36
solver.add(167*array[1] + 356*array[2] + 346*array[5] + 96*array[6] + (-76)*array[8] +
          (-57)*array[9] + 452*array[10] + (-159)*array[11] + 276*array[12] + (-168)*array[13] +
          (-207)*array[16] + 232*array[17] + 250*array[20] + 148*array[21] + 146*array[22] +
          (-165)*array[23] + 37*array[25] + 153*array[27] + (-109)*array[28] + 356*array[30] +
          (-173)*array[31] + 112*array[32] + 14*array[33] + 344*array[35] + 79*array[36] == 233261)

# boolExpr37
solver.add(237*array[0] + 430*array[4] + (-221)*array[6] + 188*array[7] + 67*array[11] +
          98*array[12] + 450*array[13] + 177*array[14] + 135*array[16] + 384*array[18] +
          (-74)*array[19] + 66*array[20] + (-220)*array[22] + 342*array[23] + 378*array[24] +
          (-223)*array[25] + 238*array[26] + 263*array[27] + (-15)*array[28] + 141*array[29] +
          368*array[31] + 111*array[32] + 305*array[33] + 430*array[34] + 350*array[36] == 377006)

# 添加约束：所有变量都是ASCII可打印字符
# for i in range(37):
#     solver.add(32 <= array[i], array[i] <= 126)

# 求解方程组
if solver.check() == sat:
    model = solver.model()
    # 获取解并转换为字符
    flag = ''
    for i in range(37):
        flag += chr(model[array[i]].as_long())
    print("Flag:", flag)
else:
    print("无解")

Flag: TSCTF-J{N0w_L3t’s_7ry_T4ble_Tenni5^^}

iPlayCalc

查到upx壳

image-20250911143228699

懒得用动调脱壳了，直接上工具XVolkolak

脱壳成功

IDA打开发现一大堆base64串，和码表

应该是做了个base64解码，动调跟进去发现

image-20250911144850862

仿射加密

1
E(x) = (ax + b) mod 26

解密：

1
D(y) = a^(-1) * (y - b) mod 26
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
def mod_inverse(a, m):
    """计算a在模m下的乘法逆元"""
    for i in range(1, m):
        if (a * i) % m == 1:
            return i
    return None


def affine_decrypt(ciphertext, a, b):
    """使用仿射密码解密"""
    plaintext = ""
    a_inv = mod_inverse(a, 26)  # 计算a的乘法逆元

    for char in ciphertext:
        if 'A' <= char <= 'Z':  # 大写字母
            # 将字符转换为0-25的数字
            num = ord(char) - ord('A')
            # 应用解密公式: D(y) = a^(-1) * (y - b) mod 26
            decrypted = (a_inv * (num - b)) % 26
            # 转换回字符
            plaintext += chr(decrypted + ord('A'))
        elif 'a' <= char <= 'z':  # 小写字母
            # 将字符转换为0-25的数字
            num = ord(char) - ord('a')
            # 应用解密公式: D(y) = a^(-1) * (y - b) mod 26
            decrypted = (a_inv * (num - b)) % 26
            # 转换回字符
            plaintext += chr(decrypted + ord('a'))
        else:  # 非字母字符保持不变
            plaintext += char

    return plaintext


# 目标密文
ciphertext = "MJNMW-I{Chm3_N0pgjt_Qtj1zu}"

# 仿射密码参数
a = 3
b = 7

# 解密
flag = affine_decrypt(ciphertext, a, b)
print("解密后的flag:", flag)

解密后的flag: TSCTF-J{Hat3_C0urse_Des1gn}

iPlayTarot

c# ,dnspy打开

发现click里的主逻辑

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
# 打开文件并读取每行内容
hex_values = []
with open("a.txt", "r") as file:
    for line in file:
        # 移除每行的换行符，并将十六进制字符串转换为整数
        hex_values.append(int(line.strip(), 16))

# 打印列表
print(hex_values)

enc = [49, 48, 49, 50, 48, 50, 50, 48, 57, 49, 48, 57, 50, 48, 52, 49, 48, 57, 48, 48, 48, 51, 48, 55, 51, 48, 52, 48, 48, 52, 51, 48, 51, 51, 48, 52, 48, 48, 53, 48, 48, 48, 50, 48, 51, 48, 48, 51, 51, 48, 53, 50, 48, 56, 48, 48, 48, 50, 48, 54, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 54, 50, 48, 56, 48, 48, 48, 48, 48, 48, 48, 48, 55, 48, 48, 48, 48, 48, 50, 50, 48, 57, 48, 48, 51, 51, 48, 56, 51, 48, 55, 51, 48, 49, 51, 48, 49, 48, 48, 48, 48, 48, 48, 50, 48, 53, 48, 48, 48, 48, 48, 48, 48, 48, 48, 50, 48, 49, 51, 48, 54, 48, 48, 48, 50, 48, 54, 48, 48, 48, 50, 48, 52, 48, 48, 48, 48, 48, 55, 48, 48, 48, 48, 48, 48, 51, 48, 54, 49, 48, 49, 51, 48, 50, 48, 48, 54, 51, 48, 57, 50, 57, 53, 50, 48, 51, 48, 48, 48, 50, 48, 49, 48, 48, 52, 50, 48, 55, 51, 48, 56, 51, 57, 53, 48, 48, 48, 51, 48, 51, 50, 48, 55, 50, 48, 50, 48, 48, 53, 48, 48, 50, 48, 48, 48, 51, 48, 57, 48, 48, 48, 48, 48, 49, 48, 48, 48, 51, 48, 50, 48, 48, 49]


# 将整数数组 enc 转换为字符列表
chars = [chr(i) for i in enc]

# 创建一个新的字符串数组，存储每3个字符组合的字符串
array3 = ["" for _ in range(len(enc) // 3)]

for j in range(len(array3)):
    text = chr(enc[j * 3])
    text2 = chr(enc[j * 3 + 1])
    text3 = chr(enc[j * 3 + 2])
    array3[j] = text + text2 + text3

# 输出结果
print(array3)

# 初始化 Tarot.isCardSelected 字典
isCardSelected = {
    "000": False, "001": False, "002": False, "003": False, "004": False,
    "005": False, "006": False, "007": False, "008": False, "009": False,
    "010": False, "011": False, "012": True, "013": False, "014": False,
    "015": False, "016": False, "017": False, "018": False, "019": False,
    "020": False, "021": False, "101": False, "102": False, "103": False,
    "104": False, "105": False, "106": False, "107": False, "108": False,
    "109": False, "110": False, "111": False, "112": False, "113": False,
    "114": False, "201": False, "202": False, "203": False, "204": False,
    "205": False, "206": False, "207": False, "208": False, "209": False,
    "210": False, "211": False, "212": False, "213": False, "214": False,
    "301": False, "302": False, "303": False, "304": False, "305": False,
    "306": False, "307": False, "308": False, "309": False, "310": False,
    "311": False, "312": False, "313": False, "314": False, "401": False,
    "402": False, "403": False, "404": False, "405": False, "406": True,
    "407": False, "408": False, "409": False, "410": False, "411": False,
    "412": False, "413": False, "414": False, "": False
}

# 创建一个新的字典
dictionary = {}

# 获取 Tarot.isCardSelected 字典的所有键（Keys）
keys = list(isCardSelected.keys())

# 遍历键并将其与 array3 中的元素配对，存入 dictionary
for k in range(len(keys) - 1):  # -1 是为了避免越界错误
    dictionary[keys[k]] = array3[k]

# 输出结果
print(dictionary)
# {'000': '101', '001': '202', '002': '209', '003': '109', '004': '204', '005': '109', '006': '000', '007': '307', '008': '304', '009': '004', '010': '303', '011': '304', '012': '005', '013': '000', '014': '203', '015': '003', '016': '305', '017': '208', '018': '000', '019': '206', '020': '000', '021': '000', '101': '000', '102': '006', '103': '208', '104': '000', '105': '000', '106': '007', '107': '000', '108': '002', '109': '209', '110': '003', '111': '308', '112': '307', '113': '301', '114': '301', '201': '000', '202': '000', '203': '205', '204': '000', '205': '000', '206': '000', '207': '201', '208': '306', '209': '000', '210': '206', '211': '000', '212': '204', '213': '000', '214': '007', '301': '000', '302': '000', '303': '306', '304': '101', '305': '302', '306': '006', '307': '309', '308': '295', '309': '203', '310': '000', '311': '201', '312': '004', '313': '207', '314': '308', '401': '395', '402': '000', '403': '303', '404': '207', '405': '202', '406': '005', '407': '002', '408': '000', '409': '309', '410': '000', '411': '001', '412': '000', '413': '302', '414': '001'}

靠上面的dict理解

1
2
3
4
5
string[] array6 = new string[16];
for (int l = 0; l < array6.Length; l++)
{
	array6[l] = dictionary[Tarot.SelectedCards[l]];
}

输入的应该记录在了selectedcards里了，16张牌，如”000”

比如输入[‘000’],那么array6[0]=’101’根据上面的关系

之后再来看check方法

首先不能有000，以下肯定不能选

1
006,013,018,020,021,101,104,105,107,201,202,204,205,206,209,211,213,301,302,310,402,408,410,412,
1
{'000': '101', '001': '202', '002': '209', '003': '109', '004': '204', '005': '109', '007': '307', '008': '304', '009': '004', '010': '303', '011': '304', '012': '005', '014': '203', '015': '003', '016': '305', '017': '208', '019': '206', '102': '006', '103': '208', '106': '007', '108': '002', '109': '209', '110': '003', '111': '308', '112': '307', '113': '301', '114': '301', '203': '205', '207': '201', '208': '306', '210': '206', '212': '204', '214': '007', '303': '306', '304': '101', '305': '302', '306': '006', '307': '309', '308': '295', '309': '203', '311': '201', '312': '004', '313': '207', '314': '308', '401': '395', '403': '303', '404': '207', '405': '202', '406': '005', '407': '002', '409': '309', '411': '001', '413': '302', '414': '001'}
1
2
3
4
5
6
7
8
9
10
11
public CheckClass(string[] m0)
{
    for (int i = 0; i < 14; i++)
    {
        this.m[i] = m0[i];  // 将传入的数组 m0 的前 14 个元素赋值给 m
    }
    this.dora[0] = m0[14];
    this.dora[1] = m0[15];
    Array.Sort<string>(this.m);  // 对 m 数组进行排序
    // 后续的代码将对 m 进行处理
}

check000，check201，check004至少达成一种

大致看了下终于看懂了，fold的值要>13或者其他的一些情况才能输出flag

1
2
3
4
5
6
7
8
9
10
11
12
private void CheckDora2()
{
	string[] array = this.dora;
	for (int i = 0; i < array.Length; i++)
	{
		if (array[i] == "004")
		{
			this.fold++;
			Console.WriteLine("Dora2");
		}
	}
}

两张dora里有一个004fold++

1
109,312,009
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
private void CheckDora1()
{
	for (int i = 0; i < this.m.Length; i++)
	{
		if (this.m[i][1] == '9')
		{
			this.fold++;
			Console.WriteLine("Dora1");
			StringBuilder stringBuilder = new StringBuilder(this.m[i]);
			stringBuilder[1] = '0';
			this.m[i] = stringBuilder.ToString();
		}
	}
	this.Counts = new Dictionary<string, int>();
	foreach (string text in this.m)
	{
		if (!this.Counts.ContainsKey(text))
		{
			this.Counts[text] = 0;
		}
		Dictionary<string, int> counts = this.Counts;
		string text2 = text;
		int num = counts[text2];
		counts[text2] = num + 1;
	}
}

如果中间为9则替换成0，同时fold++

同时计算m中字符串出现的次数

1
295,395

check000做了什么，问了gpt

这完全像麻将里的“胡牌检查”算法：

  • 先找“雀头”（对子）
  • 再检查剩下牌能否组成刻子或顺子
  • 如果可以，全组合有效，返回 true
  • 这三个必须满足一个才能胡牌
1
2
3
001-001   // 对子
002-003-004 // 顺子
005-005-005 // 刻子

check201找是不是有7个对子

fold+2

check004

当执行 Check004() 方法时，hashSet 和 hashSet2 都包含相同的元素，满足 hashSet.IsSubsetOf(hashSet2) 和 hashSet2.IsSubsetOf(hashSet) 条件，因此返回 true。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
private void Check101()
{
	Dictionary<string, int> dictionary = new Dictionary<string, int>();
	foreach (string text in this.SCounts)
	{
		if (!dictionary.ContainsKey(text))
		{
			dictionary[text] = 0;
		}
		Dictionary<string, int> dictionary2 = dictionary;
		string text2 = text;
		int num = dictionary2[text2];
		dictionary2[text2] = num + 1;
	}
	if (dictionary.Values.ToArray<int>().Count((int x) => x == 2) == 1)
	{
		this.fold++;
		Console.WriteLine("101");
	}
}
1
this.SCounts = new List<string> { "001-002-003", "004-005-006", "001-002-003" };

出现次数为 2 的元素有 1 个 → 条件满足 → fold+1 → 打印 "101"

Check101() 是在判断 SCounts 里是否正好有一个对子（出现两次的组合），如果有就增加 fold 并打印 "101"。

check102

1
2
3
4
5
6
7
8
9
10
11
12
private void Check102()
{
	foreach (string text in this.m)
	{
		if (text.StartsWith("0") || text.EndsWith("1") || text.EndsWith("9"))
		{
			return;
		}
	}
	this.fold++;
	Console.WriteLine("102");
}

只要有一个start为0或end为1或9的就fold++

check103:

1
2
3
4
5
6
7
8
9
10
11
12
13
private void Check103()
{
	for (int i = 0; i <= this.m.Length - 3; i++)
	{
		if (this.m[i].StartsWith("0") && this.m[i] == this.m[i + 1] && this.m[i] == this.m[i + 2])
		{
			this.fold++;
			Console.WriteLine("103");
			i += 2;
		}
	}
}

判断当前元素是否以 “0” 开头，并且当前元素与下一个和下下一个元素相同

check202

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
^：表示匹配字符串的开始位置。
(00\\d-00\\d)：
00：匹配字符 00。
\\d：匹配一个数字（0-9），\\d 是转义符，表示数字字符。
-：匹配字符 -。
所以，这部分的意思是：一个字符串形如 "00x-00x"，其中 x 是任意数字。
(00\\d-00\\d-00\\d)：
这部分匹配一个形如 "00x-00x-00x" 的字符串，其中每个 x 是任意数字。
(\\d01-\\d01)：
\\d：表示任意数字。
01：表示数字 01。
所以，这部分匹配一个形如 "01-01" 的字符串。
(\\d09-\\d09)：
与上面类似，匹配形如 "09-09" 的字符串。
(\\d01-\\d01-\\d01)：
匹配形如 "01-01-01" 的字符串。
(\\d09-\\d09-\\d09)：
匹配形如 "09-09-09" 的字符串。
(\\d01-\\d02-\\d03)：
匹配形如 "01-02-03" 的字符串。
(\\d07-\\d08-\\d09)：
匹配形如 "07-08-09" 的字符串。
$：表示匹配字符串的结束位置。

check203

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
private void Check203()
{
	HashSet<string> hashSet = new HashSet<string>();
	hashSet.Add("101-102-103 104-105-106 107-108-109");
	hashSet.Add("201-202-203 204-205-206 207-208-209");
	hashSet.Add("301-302-303 304-305-306 307-308-309");
	HashSet<string> SCountsSet = new HashSet<string>(this.SCounts);
	Func<string, bool> <>9__0;
	foreach (string text in hashSet)
	{
		IEnumerable<string> enumerable = text.Split(new char[] { ' ' });
		Func<string, bool> func;
		if ((func = <>9__0) == null)
		{
			func = (<>9__0 = (string part) => SCountsSet.Contains(part));
		}
		if (enumerable.All(func))
		{
			this.fold += 2;
			Console.WriteLine("203");
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
遍历 hashSet 中的每个卡片组合。例如，"101-102-103 104-105-106 107-108-109"。

IEnumerable<string> enumerable = text.Split(new char[] { ' ' });

使用空格 (" ") 来拆分每个组合中的卡片。例如，将 "101-102-103 104-105-106 107-108-109" 拆分成三个部分："101-102-103", "104-105-106", "107-108-109"。

if (enumerable.All(func))

All() 方法检查每个部分是否都存在于 SCountsSet 中。如果所有拆分出来的卡片组合都在 SCountsSet 中，则返回 true。

this.fold += 2;

如果当前组合中的所有卡片都存在于 SCountsSet 中，增加 fold 的值（fold 是一个计数器，表示符合条件的组合次数）。

check204,check205,check208, Check006都与203类似

check206

正则表达式的作用是检查字符串是否符合以下两种格式之一：

  • **^(\\d{3})-(\\1)-(\\1)$**：表示一个字符串是形如 "xxx-xxx-xxx" 的格式，其中 xxx 为三位数字，并且第二和第三部分的数字必须和第一部分相同。
    • 例如："001-001-001", "123-123-123", "555-555-555"。
  • **^(\\d{3})-(\\2)$**：表示字符串是形如 "xxx-yyy" 的格式，其中 xxx 是三位数字，而 yyy 是第二部分（\\2）与第一部分相同。
    • 例如："123-123", "001-001", "009-009"。

check207

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
private void Check207()
{
	if (!Array.Exists<string>(this.m, (string s) => s.StartsWith("0")))
	{
		return;
	}
	foreach (string text in this.m)
	{
		if (!text.StartsWith("0") && !text.EndsWith("1") && !text.EndsWith("9"))
		{
			return;
		}
	}
	this.fold += 2;
	Console.WriteLine("207");
}

先查看是否start=0，如果所有元素都以 “0” 开头，且要么以 “1” 结尾，要么以 “9” 结尾 fold+=2

看到这心态略崩…

1
2
3
4
5
6
7
8
private void Check301()
{
	if (this.SCounts.Count != 0 && this.Check201())
	{
		this.fold += 3;
		Console.WriteLine("301");
	}
}

check302

1
2
3
4
5
6
7
8
9
10
11
\\d01-\\d01：形如 01-01 的格式。

\\d09-\\d09：形如 09-09 的格式。

\\d01-\\d01-\\d01：形如 01-01-01 的格式。

\\d09-\\d09-\\d09：形如 09-09-09 的格式。

\\d01-\\d02-\\d03：形如 01-02-03 的格式。

\\d07-\\d08-\\d09：形如 07-08-09 的格式。

check303:// 检查 m 数组中的首字母是否有两个不同的字符

1
2
经过 .Select((string s) => s[0]) 后，我们提取的首字母数组是 ['0', '0', '1', '1', '2']。
使用 Distinct() 后得到的唯一字符是 ['0', '1', '2']，即共有 3 个不同的字符。

check601:// 检查 m 数组中的首字母是否只有一个不同的字符

剩下的缓缓

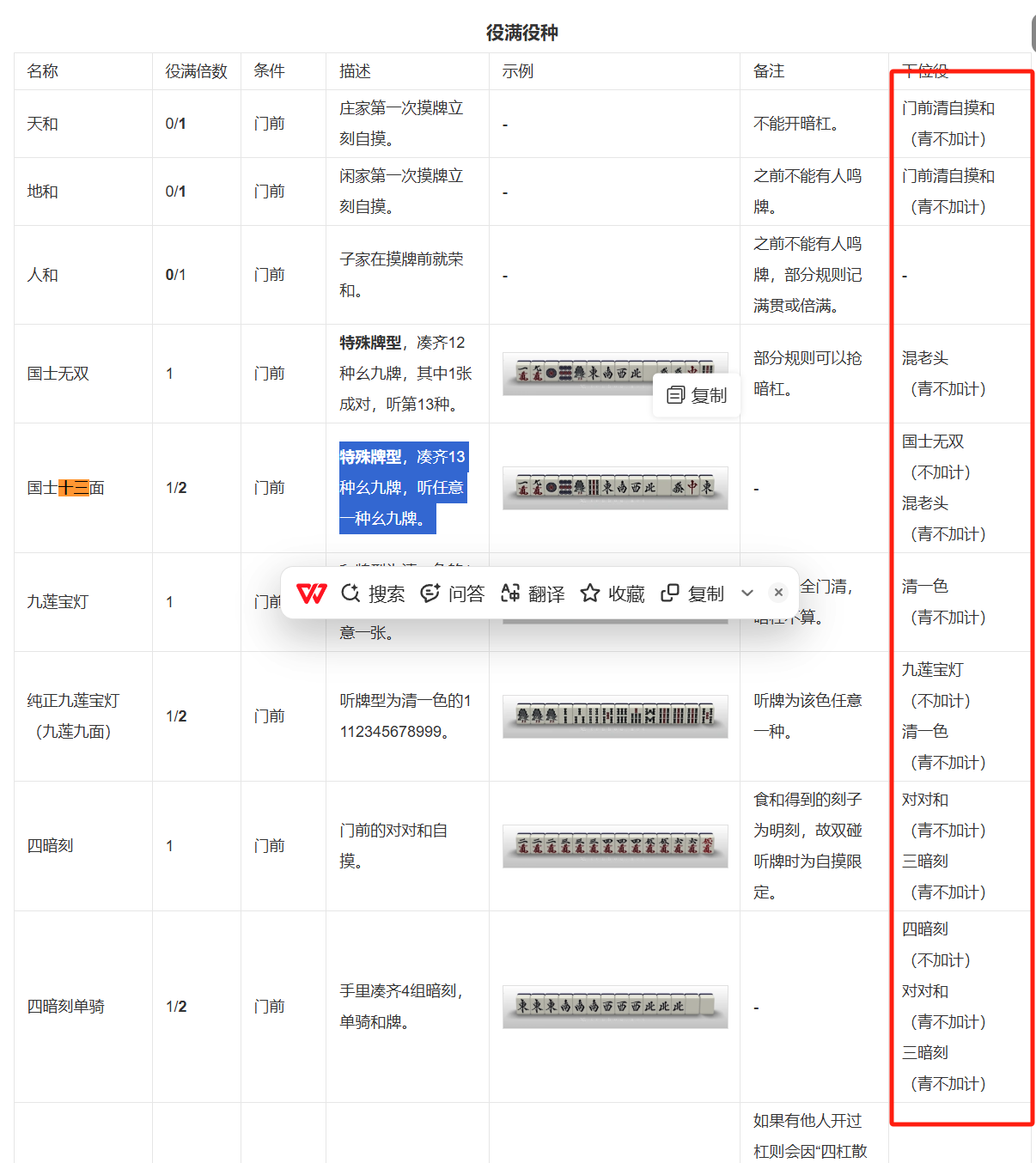
出题人说了是日本麻将牌，那么先读懂规则把…

日本麻将_百度百科

日本麻将的牌由三门数牌（万/饼/索，1~9）和字牌（东南西北中白发）组成，常见基本和牌结构是“4个面子+1雀头”（面子为刻子或顺子），另有七对子、十三幺等特殊手型。计分依赖役种与宝牌（Dora）等加成。

16张牌经映射后进入校验类的构造函数：前14张是主体牌，后2张是“dora”牌。

入口：若任何一张是“000”（非法/空）直接失败并弹窗“百事无成，功亏一篑。”。然后处理两段 dora（见上），更新 fold 与 Counts。

基础门槛：若不满足“基本四面子一雀头”（Check000）、“七对子”（Check201）、“十三幺”（Check004）三者之一，则直接失败。也就是说，和牌必须是基本形或两大特殊形其一。

看了规则之后发现

image-20250912201207903

这种役都能对上那些话，如水天一色，绿意盎然和清一色

在日本麻将中，宝牌是用于计算额外得分的牌，它通常与某些特定的牌（如“宝牌”或者“翻数”）相关。例如，如果一个玩家的胡牌包括宝牌，那么这个玩家的得分就会增加 宝牌数量 * 2 的分数。如果玩家在胡牌时能够“碰”或“杠”宝牌，那么这些宝牌的数量会被纳入最终得分计算中。例如，宝牌（Dora）增加得分的规则是每一张宝牌为玩家增加一番。

假设玩家的手牌是一个平和（没有任何番型的基本胡牌）且有一张宝牌。例如玩家胡牌时有一张 "5"，并且系统选择的宝牌也是 "5"，那么该玩家的得分会因宝牌的加入而增加番数。

Dora 加成与折算分 fold

CheckDora1：若主体牌中存在“第二位字符为‘9’”的牌就 fold++，且把该位改成‘0’后重算 Counts（相当于以某种指示器把牌当成另一值，具体机制不按规则书而是题目特设）。

随后 CheckDora2：若两张 dora 中存在“004”则 fold++。这些都是在加“额外分数”。（这部分是出题人自定义的“Dora 加番”，不完全等价于标准立直麻将 Dora 机制。）引用位置见构造与方法区域。

基础和牌结构（四面子一雀头）的判定

核心在三个方法：尝试所有可能的雀头（对子）后，余牌是否能被拆成“刻子/顺子”。这正是日麻“4面子+1雀头”的基本结构。 Check000 Check00 Check0 1

  • Check000：枚举 Counts 里所有张数≥2的牌作为雀头，拷贝一份计数减去这对，调用 Check00 尝试把余牌拆完；若成功记录拆分列表 SCounts 并返回 true。
  • Check00：循环用“优先刻子（3张相同）否则顺子（x,x+1,x+2，同花色）”的策略清空计数；顺子只允许数牌

这些拆分产生的面子字符串被放进 SCounts，后面的番种判定会基于它。

特殊和型（不走四面子一雀头）基础判定

  • 七对子（Check201）：所有牌都成对（Counts 值全为2），且先前并未生成 SCounts（即未按面子拆分），则判定为七对子成立。 Check201
  • 十三幺（Check004）：检查14张牌的“集合”恰好等于固定的13种幺九/字牌集合（1/9万饼索 + 东南西北中白发中的组合），等价于14张由13种各1张加任意其中1张作将。

番种/役种的具体判定（都建立在“已经是可和型”基础上）

通过基础门槛后，会用一系列 Check1xx/2xx/3xx/6xx 给 fold 加分，或直接判定为某个“特殊役”并弹窗返回，fold>13或者通过那些特殊役

Check001：绿一色（“水天一色，绿意盎然。”）。要求 SCounts 里每个面子都只能是 202/203/204/206/208/006（即发/索中若干绿牌）的对/刻/顺之一，对应日麻“绿一色”。

面子：顺子、刻子、杠子的统称。

Check002：清老头（“老练清和，智胜难关。”）。要求无字牌且每张都是1或9（末位为1或9），对应“清老头”。 清老头指的是玩家的胡牌全部由“1”和“9”组成，且没有其他任何数字牌。

Check003：字一色（“天机独运，字字生辉。”）。要求至少有字牌，且所有牌第一位字符相同且为‘0’，即全是字牌。对应“字一色”。

Check004：十三幺（“运筹帷幄，国士之风。”），已在上面解释。

Check005：九莲宝灯（“华灯璀璨，九运亨通。”）。要求清一色且张数分布恰为 1112345678999x（x任意同门一张），代码里根据门别分别要求 1和9至少3张，2~8各至少1张。对应“九莲宝灯”。

Check006：四喜（“吉星高照，喜从天降。”）。枚举了四风（001~004）中“3副刻子+1对”或“四副刻子”的模式（小四喜/大四喜）。

Check007：大三元（“三元及第，一品当朝。”）。要求 005/006/007 各一副刻子（白/发/中三元）。

其他“加分役”示例：

  • Check101：若 SCounts 中某个面子字符串恰好出现两次（同面子重复一次）则 fold++，相当于“一杯口”风味。
  • Check102：所有牌都不是字牌且不含1/9，即“断幺九”风味（全是中张），fold++。
  • Check103：存在字牌的刻子（连续三张相同的字牌），fold++。
  • Check202：混全带幺九风味（每个面子都带幺九或字牌，且手牌里含有字牌），fold+=2。
  • Check203：一气通贯（同门 123/456/789 三顺齐全），fold+=2。
  • 还有 Check204~Check303、Check601 等，分别给不同条件加分或清一色加高分等。

最后反正是满足得输入做了md5加密为最终答案，我们需要由最终的True反推可行的输入去做MD5

烦就烦在不一定所有的役可行，而且判定复杂头大….，外部的ID和内部ID容易搞混，真实屎完了

1
{'000': '101', '001': '202', '002': '209', '003': '109', '004': '204', '005': '109', '007': '307', '008': '304', '009': '004', '010': '303', '011': '304', '012': '005', '014': '203', '015': '003', '016': '305', '017': '208', '019': '206', '102': '006', '103': '208', '106': '007', '108': '002', '109': '209', '110': '003', '111': '308', '112': '307', '113': '301', '114': '301', '203': '205', '207': '201', '208': '306', '210': '206', '212': '204', '214': '007', '303': '306', '304': '101', '305': '302', '306': '006', '307': '309', '308': '295', '309': '203', '311': '201', '312': '004', '313': '207', '314': '308', '401': '395', '403': '303', '404': '207', '405': '202', '406': '005', '407': '002', '409': '309', '411': '001', '413': '302', '414': '001'}

我们发现10x只有101和109，少了7张牌，其它的2xx和3xx都是各有两张，东南西北中发也是各有两张

需要刻字的我们直接pass，check007，006，005,002,001都不行,还要注意之前True的两个012，406是被禁用的(也就是005)

1
{'000': '101', '001': '202', '002': '209', '003': '109', '004': '204', '005': '109', '007': '307', '008': '304', '009': '004', '010': '303', '011': '304', '014': '203', '015': '003', '016': '305', '017': '208', '019': '206', '102': '006', '103': '208', '106': '007', '108': '002', '109': '209', '110': '003', '111': '308', '112': '307', '113': '301', '114': '301', '203': '205', '207': '201', '208': '306', '210': '206', '212': '204', '214': '007', '303': '306', '304': '101', '305': '302', '306': '006', '307': '309', '308': '295', '309': '203', '311': '201', '312': '004', '313': '207', '314': '308', '401': '395', '403': '303', '404': '207', '405': '202',  '407': '002', '409': '309', '411': '001', '413': '302', '414': '001'}

十三幺也不行了check004,字一色也不行check003,

我们发现符合的场景最简单的就是7对子，但是发现了题目的BUG

就是说当7对子情况下，拆面子失败check000会return false,scounts为空，去执行check201，这时check001可以直接返回true，因为scounts是空的

接下来就是算分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
if (new CheckClass(array6).Check())
{
	string text3 = string.Join("", Tarot.SelectedCards.OrderBy((string card) => card).ToArray<string>());
	using (MD5 md = MD5.Create())
	{
		byte[] array7 = md.ComputeHash(Encoding.UTF8.GetBytes(text3));
		StringBuilder stringBuilder = new StringBuilder();
		foreach (byte b in array7)
		{
			stringBuilder.Append(b.ToString("x2"));
		}
		text3 = stringBuilder.ToString();
	}
	MessageBox.Show("TSCTF-J{" + text3 + "}", "Flag", MessageBoxButtons.OK, MessageBoxIcon.Asterisk);
	return;
}

是按值进行排序，

TSCTF-J{ba5c5c1e0ff96f0485d5fd00ddc31077}

照理说这个flag能出，但是错误了

询问出题人，才发现这是一个bug，没有在check001之前做校验

正确的思路应该是算分来获得flag

首先验证了下7对子是无法到达13分的，最多能到12分

高分叠加方案：

check102不以0开头，19结尾，1分

check301(7对子，但是可以拆出面子) 3分

check601，6分

此时还有dora没算

仔细阅读规则发现有部分牌如295(其实就是205)

可以加1分

两个004可以加2分

这样刚好13分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
# 打开文件并读取每行内容
hex_values = []
with open("a.txt", "r") as file:
    for line in file:
        # 移除每行的换行符，并将十六进制字符串转换为整数
        hex_values.append(int(line.strip(), 16))

# 打印列表
print(hex_values)

enc = [49, 48, 49, 50, 48, 50, 50, 48, 57, 49, 48, 57, 50, 48, 52, 49, 48, 57, 48, 48, 48, 51, 48, 55, 51, 48, 52, 48, 48, 52, 51, 48, 51, 51, 48, 52, 48, 48, 53, 48, 48, 48, 50, 48, 51, 48, 48, 51, 51, 48, 53, 50, 48, 56, 48, 48, 48, 50, 48, 54, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 54, 50, 48, 56, 48, 48, 48, 48, 48, 48, 48, 48, 55, 48, 48, 48, 48, 48, 50, 50, 48, 57, 48, 48, 51, 51, 48, 56, 51, 48, 55, 51, 48, 49, 51, 48, 49, 48, 48, 48, 48, 48, 48, 50, 48, 53, 48, 48, 48, 48, 48, 48, 48, 48, 48, 50, 48, 49, 51, 48, 54, 48, 48, 48, 50, 48, 54, 48, 48, 48, 50, 48, 52, 48, 48, 48, 48, 48, 55, 48, 48, 48, 48, 48, 48, 51, 48, 54, 49, 48, 49, 51, 48, 50, 48, 48, 54, 51, 48, 57, 50, 57, 53, 50, 48, 51, 48, 48, 48, 50, 48, 49, 48, 48, 52, 50, 48, 55, 51, 48, 56, 51, 57, 53, 48, 48, 48, 51, 48, 51, 50, 48, 55, 50, 48, 50, 48, 48, 53, 48, 48, 50, 48, 48, 48, 51, 48, 57, 48, 48, 48, 48, 48, 49, 48, 48, 48, 51, 48, 50, 48, 48, 49]


# 将整数数组 enc 转换为字符列表
chars = [chr(i) for i in enc]

# 创建一个新的字符串数组，存储每3个字符组合的字符串
array3 = ["" for _ in range(len(enc) // 3)]

for j in range(len(array3)):
    text = chr(enc[j * 3])
    text2 = chr(enc[j * 3 + 1])
    text3 = chr(enc[j * 3 + 2])
    array3[j] = text + text2 + text3

# 输出结果
print(array3)

# 初始化 Tarot.isCardSelected 字典
isCardSelected = {
    "000": False, "001": False, "002": False, "003": False, "004": False,
    "005": False, "006": False, "007": False, "008": False, "009": False,
    "010": False, "011": False, "012": True, "013": False, "014": False,
    "015": False, "016": False, "017": False, "018": False, "019": False,
    "020": False, "021": False, "101": False, "102": False, "103": False,
    "104": False, "105": False, "106": False, "107": False, "108": False,
    "109": False, "110": False, "111": False, "112": False, "113": False,
    "114": False, "201": False, "202": False, "203": False, "204": False,
    "205": False, "206": False, "207": False, "208": False, "209": False,
    "210": False, "211": False, "212": False, "213": False, "214": False,
    "301": False, "302": False, "303": False, "304": False, "305": False,
    "306": False, "307": False, "308": False, "309": False, "310": False,
    "311": False, "312": False, "313": False, "314": False, "401": False,
    "402": False, "403": False, "404": False, "405": False, "406": True,
    "407": False, "408": False, "409": False, "410": False, "411": False,
    "412": False, "413": False, "414": False, "": False
}

# 创建一个新的字典
dictionary = {}

# 获取 Tarot.isCardSelected 字典的所有键（Keys）
keys = list(isCardSelected.keys())

# 遍历键并将其与 array3 中的元素配对，存入 dictionary
for k in range(len(keys) - 1):  # -1 是为了避免越界错误
    dictionary[keys[k]] = array3[k]

# 输出结果
print(dictionary)
print(len(dictionary))

keys_to_remove = [key for key, value in dictionary.items() if value == '000']
for key in keys_to_remove:
    del dictionary[key]

# 输出包含 '000' 的条目对应的 key
print("Keys with value '000':")
for key in keys_to_remove:
    print(key,end=',')

# 打印处理后的字典
print("\nUpdated dictionary:")
print(dictionary)

import hashlib; combos={"A":["001","405","014","309","004","212","019","210","313","404","017","103","203","308","009","312"],"B":["009","312","305","413","010","403","008","011","208","303","007","112","111","314","016","401"]};

# ['001','405','']

def show(name, arr):
    arr_sorted=sorted(arr)
    s="".join(arr_sorted)
    m=hashlib.md5(s.encode()).hexdigest()
    print(name+":")
    print("sorted=",arr_sorted)
    print("concat=",s)
    print("md5=",m)

show("A", combos["A"])
show("B", combos["B"])

# 3eff7e994979d97fca68de1e5e5197a2
# af6eae0e9f06be3549800d8615c72831

勉强做出来了花费了5+个小时时间，中间学了下日本麻将….有点搞心态的

iPlayApple

苹果逆向题

解压，看到一个reverse，IDA点进去看看

果然发现了相关信息

sub_100007584 的逻辑是：

  1. 获取用户在 textField 和 finField 两个输入框的内容。
  2. 把这两个字符串传给验证函数 sub_1000040EC（内部可能用 CryptoHelper 对比/解密）。
  3. 根据结果决定弹出成功提示还是失败提示。
  4. 用 UIAlertController 显示在界面上。

有个16b6aa2468414776d9168777f9ea281ee79e5f60a06278319dde7661d912e3a6

和amazing_ios_rev! (16字节)可能是密钥

简化伪代码：

  • s1 = textField.text
  • s2 = finField.text
  • ctx = get_flag() // 栈对象
  • ctx.crypto = CryptoHelper()
  • ctx.salt = “amazing_ios_rev!”
  • ctx.targetHex = “16b6aa2468414776d9168777f9ea281e…” // 看起来是 SHA256 的十六进制
  • ok = runCheck(ctx, s1, s2) // 由下游函数组合
  • if ok: 弹成功提示（可能还拼装显示flag）
  • else: 弹失败提示

jinrush40EC后比较重要的6C63这个方法，里面包含所用的加密方法

1
2
3
v30 = type metadata accessor for AES.GCM.SealedBox
v11 = type metadata accessor for SymmetricKey
v14 = type metadata accessor for String.Encoding

这里取 Swift Crypto 库里的类型元数据：AES.GCM.SealedBox、SymmetricKey、String.Encoding。

说明这个函数会用到 AES-GCM 来处理数据。

1
2
3
4
5
v33 = a3;
v34 = a4;
v19 = static String.Encoding.utf8.getter();
v20 = sub_100006E18(v19);
v21 = StringProtocol.data(using:allowLossyConversion:)(..., utf8)

参数 (a3,a4) 是一个 Swift String（也就是调用 sub_1000040EC 时传入的 内部常量 “amazing_ios_rev!” 或者 big hex 串）。

这里把它转成 UTF-8 的 Data，作为 SymmetricKey 的原始 key material。

1
2
3
sub_100006C30(a1,a2);
sub_1000042C4(a1,a2);
v25 = static AES.GCM.open(_:using:)(...)

image-20250913194606201

首先发现这个12字节的的有效信息

Nonce/IV – GCM 的初始向量，通常是 12 字节（96bit）。

可能就是这个头部

tag是16字节

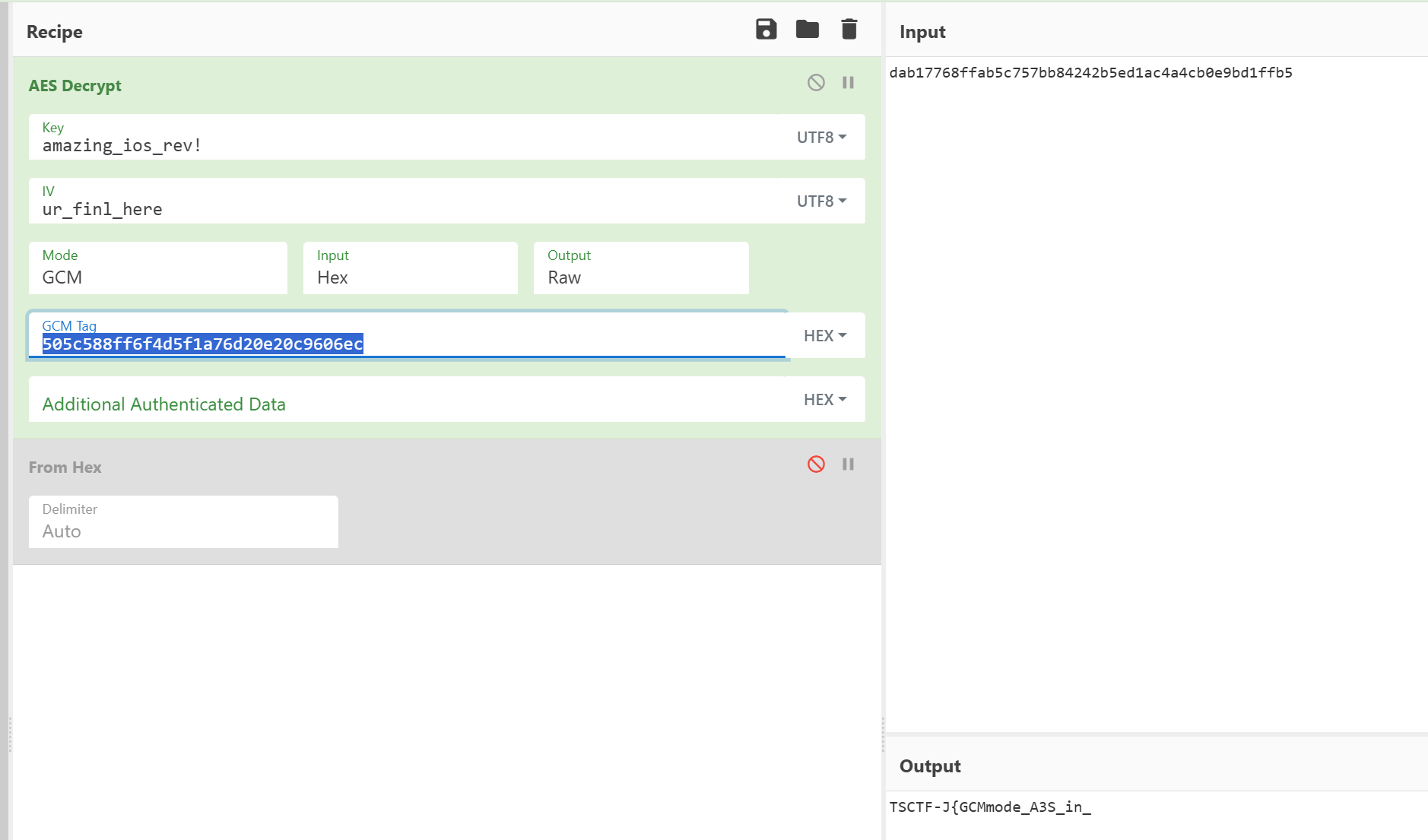
想到之前的iv是拼接的,tag可能也是拼接的，简单试了下是505c588ff6f4d5f1a76d20e20c9606ec

image-20250913195623378

最后爆破即可,因为是一个SHA256,且16b6aa2468414776d9168777f9ea281ee79e5f60a06278319dde7661d912e3a6没用上

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import hashlib
import itertools
import string

# 目标 SHA256 值
target_hash = "16b6aa2468414776d9168777f9ea281ee79e5f60a06278319dde7661d912e3a6"

# 爆破字符表
table = "0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ!_\"#$%&'()*+,-./:;<=>?@[\\]^_`{|~"

def sha256_hex(s: str) -> str:
    return hashlib.sha256(s.encode("utf-8")).hexdigest()

for length in range(1, 21):  # 从长度1到20
    print(f"[+] Testing length {length}")
    for candidate_tuple in itertools.product(table, repeat=length):
        candidate = "".join(candidate_tuple) + "}"  # } 肯定在最后
        if sha256_hex(candidate) == target_hash:
            print(f"[!] Found match: {candidate}")
            exit(0)

print("[-] No match found up to length 20.")

[!] Found match: i0S}

TSCTF-J{GCMmode_A3S_in_i0S}

iPlayBingo

WASM文件是WebAssembly的二进制格式文件，旨在通过高效的二进制指令在现代浏览器中运行。它是由高级语言（如C、C++、Rust等）编译生成的低级字节码格式，具有高性能、可移植性和安全性。

githhub用这个工具搞出来c的代码

1
./wasm2c answerChecker.wasm -o main.c

image-20250913223410291

随便看看就发现了类似tea的算法

Webassembly逆向手法-先知社区

根据这个文章

可以用gcc 编译c代码，然后把生成的.o文件拖进去分析，并且网页可以动调

image-20250914143723994

可以发现密文

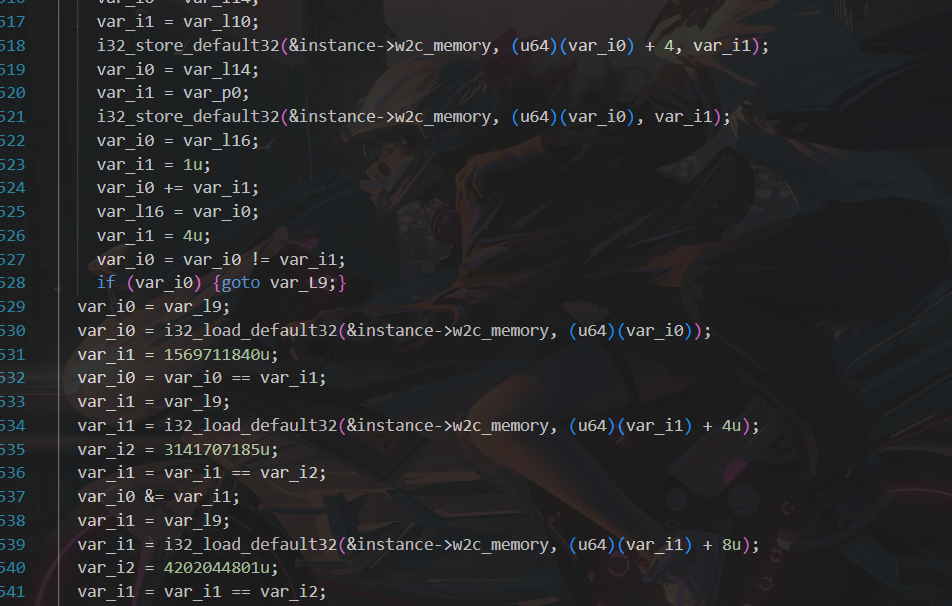
enc {0x5D8FE6E0,0xBB42A5B1,0xFA761D81,0x32CC9FCB,0xFD9BE445,0x23935C4,0xEAF80FBE,0xE52E36D3}

这段就是把32 字节输入当成 **4 个块（每块 8 字节=2×u32）处理，并且**对每个块做三段 ARX（加/减、异或、移位）轮变换**。每段都是 TEA/XTEA 的双字加密，只是换了点细节和常量。跑完三段以后，把结果写回内存。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
n31 = 31;
v24 = 0;
do {
  v24 -= 0x61C88647;                        // sum -= DELTA
  // v18 +=  F(v21) ^ ( (sum ^ v21) + (v21 ^ K[(sum>>2)&3]) )
  v18 += (((v21>>3) ^ (v21<<5)) + ((v21>>4) ^ (v21<<2)))
       ^ ((v24 ^ v21) + (v21 ^ K[(v24>>2)&3]));

  // v21 +=  ((sum ^ v18) + (K[((sum>>2)&3)^1] ^ v18)) ^ F(v18)
  v21 += ((v24 ^ v18) + (K[((v24>>2)&3)^1] ^ v18))
       ^ (((v18>>3) ^ (v18<<5)) + ((v18>>4) ^ (v18<<2)));

  v31 = n31--;
} while (v31);

key = [0x01234567, 0x89abcdef, 0xdeadbeef, 0xbabec0de]

来自

image-20250914152351513

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
n33 = 0;
v25 = 0;
do {
  // 先用当前 v25 更新 v18
  v18 += (v21 + ((v21>>5) ^ (v21<<4)))
       ^ (v25 + K[v25 & 3]);               // 这里索引还是 0..3

  v25 -= 0x61C88647;                        // 然后 sum -= DELTA

  // 再用“减完的 v25”更新 v21，子密钥索引 ((v25>>9)&0xC)+1424 其实还是选 K[ (v25>>9)&3 ]
  v21 += (v25 + K[((v25>>9) & 0xC) + 1424]) // 等价 K[(v25>>9)&3]
       ^ (v18 + ((v18>>5) ^ (v18<<4)));

  ++n33;
} while (n33 != 33);

1
2
3
4
5
6
7
8
9
10
11
12
13
for (i = 0; i != 32; ++i) {
  v33 -= 0x4686C862;                         // sum -= GAMMA

  // v18 += (16*v21 + 0x01234567) ^ ((v21>>5) - 0x76543211) ^ (v21 + v33)
  v18 += (16 * v21 + 0x01234567)
       ^ ((v21 >> 5) - 0x76543211)
       ^ (v21 + v33);

  // v21 += ((v18>>5) - 0x45413F22) ^ (v33 + v18) ^ (16*v18 - 0x21524111)
  v21 += ((v18 >> 5) - 0x45413F22)
       ^ (v33 + v18)
       ^ (16 * v18 - 0x21524111);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <stdio.h>
#include <stdint.h>
#include <iostream>

using namespace std;

void decrypt(uint32_t* v, int i) {
    uint32_t v0 = v[0], v1 = v[1];
    uint32_t key[4] = { 0x01234567, 0x89abcdef, 0xdeadbeef, 0xbabec0de };
    const uint32_t GAMMA = 0xB979379E;
    uint32_t sum = GAMMA * 32;
    for (i = 0; i < 32; i++) {
        v1 -= ((v0 << 4) + key[2]) ^ (v0 + sum) ^ ((v0 >> 5) + key[3]);
        v0 -= ((v1 << 4) + key[0]) ^ (v1 + sum) ^ ((v1 >> 5) + key[1]);
        sum -= GAMMA;
    }
    v[0] = v0;
    v[1] = v1;
}

void xteaDec(uint32_t* v) {
    uint32_t key[4] = { 0x01234567, 0x89abcdef, 0xdeadbeef, 0xbabec0de };
    uint32_t v0 = v[0], v1 = v[1], delta = 0x9e3779b9, sum = delta * 33;
    for (int i = 0; i < 33; i++) {
        v1 -= (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum >> 11) & 3]);
        sum -= delta;
        v0 -= (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
    }
    v[0] = v0;
    v[1] = v1;
}

void xxteaDec(uint32_t* v) {
    uint32_t key[4] = { 0x01234567, 0x89abcdef, 0xdeadbeef, 0xbabec0de };
    uint32_t DELTA = 0x9e3779b9;
    uint32_t sum = 32 * DELTA;
    for (int i = 0; i < 32; i++) {
        v[1] -= (((v[0] >> 4 ^ v[0] << 2) + (v[0] >> 3 ^ v[0] << 5)) ^ ((sum ^ v[0]) + (key[(1 & 3) ^ (sum >> 2 & 3)] ^ v[0])));
        v[0] -= (((v[1] >> 4 ^ v[1] << 2) + (v[1] >> 3 ^ v[1] << 5)) ^ ((sum ^ v[1]) + (key[(0 & 3) ^ (sum >> 2 & 3)] ^ v[1])));
        sum -= DELTA;
    }
}

int main() {
    uint32_t enc[8] = { 0x5D8FE6E0,0xBB42A5B1,0xFA761D81,0x32CC9FCB,0xFD9BE445,0x23935C4,0xEAF80FBE,0xE52E36D3 };
    for (int i = 0; i < 32; i += 8)
    {
        decrypt((uint32_t*)((uint8_t*)enc + i), (i + 8) / 8);
        xteaDec((uint32_t*)((uint8_t*)enc + i));
        xxteaDec((uint32_t*)((uint8_t*)enc + i));
    }

    for (int i = 0; i < 8; i++) {
        for (int j = 3; j >= 0; j--) {
            printf("%c", *((char*)&enc[i] + j));
        }
    }
    return 0;
}

TSCTF-J{Wh4t_@_R3verse_Ma5ter!!}

这里最大的坑在于第一个do_while是v28–;后缀自减，别看错了，看错浪费我很长时间

iPlayMaze

迷宫题

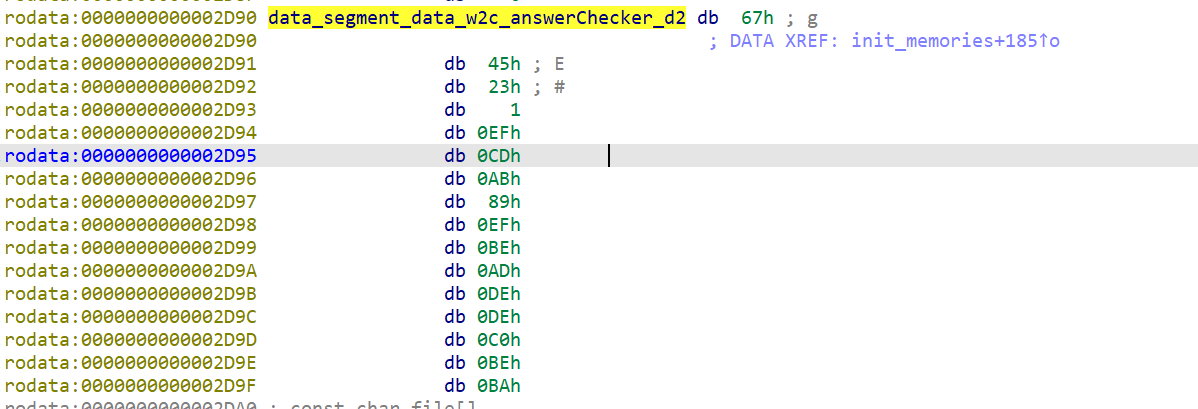
迷宫在off_405200，指向unk_405000，每8位1个有效值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
enc = [0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x1,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x1,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x1,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x1,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x1,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x1,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x1,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x1,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x1,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x1,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x1,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0]
print(len(enc))
for z in range(8):
    print(f"z={z}")
    for y in range(8):
        row = []
        for x in range(8):
            idx = z*64 + y*8 + x
            row.append('#' if enc[idx] else '.')
        print(''.join(row))
    print()

from collections import deque

moves = {
    'a': -1,
    'd': +1,
    'w': -8,
    's': +8,
    'n': -64,
    'u': +64,
}

def slide(pos, move):
    while True:
        new = pos + move
        if new < 0 or new >= 512:
            return None  # 越界
        if enc[new]:  # 碰墙
            return pos  # 停在当前位置
        pos = new

def bfs(start=0, goal=409):
    q = deque([(start,"")])
    seen = {start}
    while q:
        pos, path = q.popleft()
        if pos == goal:
            return path
        for c, delta in moves.items():
            newpos = slide(pos, delta)
            if newpos is not None and newpos not in seen:
                seen.add(newpos)
                q.append((newpos, path+c))

path = bfs()
print("solution:", path)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
512
z=0
.......#
........
........
......#.
........
........
........
........

z=1
........
........
........
........
........
...#....
........
........

z=2
........
........
.......#
........
........
........
........
........

z=3
........
........
........
........
........
........
.#......
........

z=4
........
....#...
........
#.......
........
........
........
........

z=5
........
........
........
........
........
........
........
........

z=6
........
........
#.......
#.......
........
........
........
........

z=7
........
........
........
......#.
........
......#.
........
........

solution: suawdwdsa

结果是错的

起点是0，终点是409

然后发现TLS中藏东西了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
void *__stdcall TlsCallback_0(int a1, int a2, int a3)
{
  void *result; // eax
  int i; // [esp+0h] [ebp-10Ch]
  DWORD flOldProtect; // [esp+4h] [ebp-108h] BYREF
  _BYTE v6[256]; // [esp+8h] [ebp-104h] BYREF

  v6[0] = -64;
  v6[1] = 40;
  v6[2] = -100;
  v6[3] = -112;
  v6[4] = -112;
  v6[5] = -112;
  v6[6] = 19;
  v6[7] = 80;
  v6[8] = -78;
  v6[9] = -5;
  v6[10] = 80;
  v6[11] = -88;
  v6[12] = -83;
  v6[13] = 96;
  v6[14] = -86;
  v6[15] = -110;
  v6[16] = -112;
  v6[17] = -27;
  v6[18] = -111;
  v6[19] = 83;
  v6[20] = 120;
  v6[21] = 125;
  v6[22] = 111;
  v6[23] = 111;
  v6[24] = 111;
  v6[25] = -56;
  v6[26] = 27;
  v6[27] = -99;
  v6[28] = 64;
  v6[29] = -60;
  v6[30] = -48;
  v6[31] = -112;
  v6[32] = -85;
  v6[33] = -99;
  v6[34] = 68;
  v6[35] = -60;
  v6[36] = -48;
  v6[37] = -112;
  v6[38] = -28;
  v6[39] = -11;
  v6[40] = 27;
  v6[41] = -123;
  v6[42] = 64;
  v6[43] = -60;
  v6[44] = -48;
  v6[45] = -112;
  v6[46] = 25;
  v6[47] = -123;
  v6[48] = 68;
  v6[49] = -60;
  v6[50] = -48;
  v6[51] = -112;
  v6[52] = 19;
  v6[53] = -83;
  v6[54] = -88;
  v6[55] = -60;
  v6[56] = -48;
  v6[57] = -112;
  v6[58] = -111;
  v6[59] = -27;
  v6[60] = -100;
  v6[61] = 87;
  v6[62] = 21;
  v6[63] = -68;
  v6[64] = 109;
  v6[65] = 111;
  v6[66] = 111;
  v6[67] = -110;
  v6[68] = -112;
  v6[69] = -112;
  v6[70] = -112;
  v6[71] = 123;
  v6[72] = -102;
  v6[73] = 87;
  v6[74] = 21;
  v6[75] = -68;
  v6[76] = 109;
  v6[77] = 111;
  v6[78] = 111;
  v6[79] = -111;
  v6[80] = -112;
  v6[81] = -112;
  v6[82] = -112;
  v6[83] = 27;
  v6[84] = 21;
  v6[85] = -68;
  v6[86] = 109;
  v6[87] = 111;
  v6[88] = 111;
  v6[89] = 51;
  v6[90] = -88;
  v6[91] = -60;
  v6[92] = -48;
  v6[93] = -112;
  v6[94] = 19;
  v6[95] = -83;
  v6[96] = -88;
  v6[97] = -60;
  v6[98] = -48;
  v6[99] = -112;
  v6[100] = -111;
  v6[101] = -27;
  v6[102] = -100;
  v6[103] = 87;
  v6[104] = 21;
  v6[105] = -72;
  v6[106] = 109;
  v6[107] = 111;
  v6[108] = 111;
  v6[109] = -112;
  v6[110] = -64;
  v6[111] = -48;
  v6[112] = -112;
  v6[113] = 123;
  v6[114] = -102;
  v6[115] = 87;
  v6[116] = 21;
  v6[117] = -72;
  v6[118] = 109;
  v6[119] = 111;
  v6[120] = 111;
  v6[121] = -88;
  v6[122] = -62;
  v6[123] = -48;
  v6[124] = -112;
  v6[125] = 41;
  v6[126] = -88;
  v6[127] = -62;
  v6[128] = -48;
  v6[129] = -112;
  v6[130] = 19;
  v6[131] = 121;
  v6[132] = -88;
  v6[133] = 27;
  v6[134] = 5;
  v6[135] = -72;
  v6[136] = 109;
  v6[137] = 111;
  v6[138] = 111;
  v6[139] = 25;
  v6[140] = -127;
  result = memset(&v6[141], 0, 0x73u);
  if ( a2 == 1 )
  {
    result = (void *)VirtualProtect(sub_401A60, 0x2000u, PAGE_EXECUTE_READWRITE, &flOldProtect);
    for ( i = 0; i < 141; ++i )
    {
      result = (void *)((unsigned __int8)v6[i] ^ *((unsigned __int8 *)sub_401A60 + i + 176));
      *((_BYTE *)sub_401A60 + i + 176) = (_BYTE)result;
    }
  }
  return result;
}

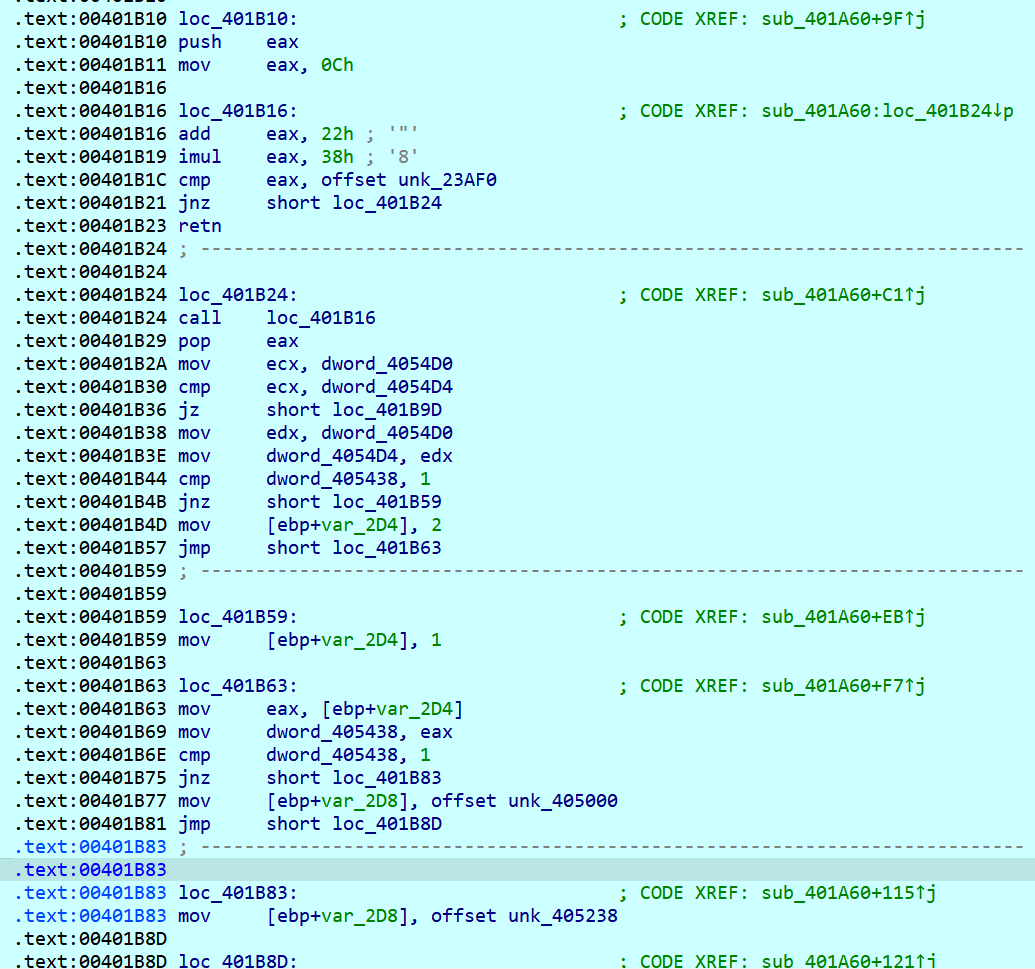
这是TLS回调在进程初始化时对一段代码做XOR解密/修补。a2==1时(进程附加)先VirtualProtect把sub_401A60附近改成可写，再用v6[0..140]依次与(sub_401A60+176+i)当前字节做异或，回填到同一地址，等于把那141字节“解密”为真正要执行的代码。静态反编译看到的是“密文”，运行后才是“明文”。若某些逻辑(含迷宫判定/校验)在这段区域里

image-20250915104950845

这块地址是我们所需关注的

image-20250915111004157

其实还有反调试，我直接用ScyllHide过了

程序存在双迷宫块:0x405000与0x405238,并非固定使用单块;每当读入一个新按键(索引自增)时,相位翻转,off_405200随之在两块之间切换

因此求解时状态应为(位置,相位)的二维状态机而不是仅512格:相位每处理一字符翻转一次;或静态打补丁固定off_405200始终指向0x405000(或0x405238)即可退化为单块迷宫

不能只看512个格子,要看1024个复合状态

写脚本的时候发现了原题是dasctf上的一个，找到脚本直接开抄了，别跟最短路径搞错了，这个是迷宫题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
maze = [0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00]

def dfs(cnt, pos, path):
    # 设置最大深度
    if cnt > 15:
        return
    if pos == 436:
        print(path)
    # a
    pos1 = pos
    if maze[pos - 1] != 1:
        while 1:
            if pos1 % 8 == 0:
                break
            if maze[pos1-1] == 1:
                dfs(cnt + 1, pos1, path + 'a')
            pos1 -= 1
    # d
    pos2 = pos
    if maze[pos + 1] != 1:
        while 1:
            if pos2 % 8 == 7:
                break
            if maze[pos2+1] == 1:
                dfs(cnt + 1, pos2, path + 'd')
            pos2 += 1
    # n
    pos3 = pos
    if maze[pos - 64] != 1:
        while 1:
            if pos3 < 64:
                break
            if maze[pos3-64] == 1:
                dfs(cnt + 1, pos3, path + 'n')
            pos3 -= 64
    # u
    pos4 = pos
    if maze[pos + 64] != 1:
        while 1:
            if pos4 + 64 >= 512:
                break
            if maze[pos4+64] == 1:
                dfs(cnt + 1, pos4, path + 'u')
            pos4 += 64
    # s
    pos5 = pos
    if maze[pos + 8] != 1:
        while 1:
            if pos5 % 64 >= 56:
                break
            if maze[pos5+8] == 1:
                dfs(cnt + 1, pos5, path + 's')
            pos5 += 8
    # w
    pos6 = pos
    if maze[pos - 8] != 1:
        while 1:
            if pos6 % 64 < 8:
                break
            if maze[pos6-8] == 1:
                dfs(cnt + 1, pos6, path + 'w')
            pos6 -= 8

dfs(0, 0, '')

这是求单迷宫的，如果双迷宫就是

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
map1 = [0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00]
map2 = [0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00]
def dfs(cnt, pos, path):
    # 设置最大深度
    if cnt > 15:
        return
    if pos == 436:
        print(path)
    if cnt % 2 == 0:
        maze = map1
    else:
        maze = map2
    # a
    pos1 = pos
    if maze[pos - 1] != 1:
        while 1:
            if pos1 % 8 == 0:
                break
            if maze[pos1-1] == 1:
                dfs(cnt + 1, pos1, path + 'a')
            pos1 -= 1
    # d
    pos2 = pos
    if maze[pos + 1] != 1:
        while 1:
            if pos2 % 8 == 7:
                break
            if maze[pos2+1] == 1:
                dfs(cnt + 1, pos2, path + 'd')
            pos2 += 1
    # n
    pos3 = pos
    if maze[pos - 64] != 1:
        while 1:
            if pos3 < 64:
                break
            if maze[pos3-64] == 1:
                dfs(cnt + 1, pos3, path + 'n')
            pos3 -= 64
    # u
    pos4 = pos
    if maze[pos + 64] != 1:
        while 1:
            if pos4 + 64 >= 512:
                break
            if maze[pos4+64] == 1:
                dfs(cnt + 1, pos4, path + 'u')
            pos4 += 64
    # s
    pos5 = pos
    if maze[pos + 8] != 1:
        while 1:
            if pos5 % 64 >= 56:
                break
            if maze[pos5+8] == 1:
                dfs(cnt + 1, pos5, path + 's')
            pos5 += 8
    # w
    pos6 = pos
    if maze[pos - 8] != 1:
        while 1:
            if pos6 % 64 < 8:
                break
            if maze[pos6-8] == 1:
                dfs(cnt + 1, pos6, path + 'w')
            pos6 -= 8

dfs(0, 0, '')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
maze = [0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00]

from sys import setrecursionlimit
setrecursionlimit(10**6)

MOVES = {
    'a': -1,   # x-1
    'd': +1,   # x+1
    'w': -8,   # y-1
    's': +8,   # y+1
    'n': -64,  # z-1
    'u': +64,  # z+1
}

def in_bounds(idx):
    return 0 <= idx < 512

def can_step(pos, delta):
    #第一步越界直接不行
    nxt = pos + delta
    if not in_bounds(nxt):
        return False
    #侧向保持行/列/层一致
    if delta == -1 and pos % 8 == 0: return False
    if delta == +1 and pos % 8 == 7: return False
    if delta == -8 and (pos % 64) < 8: return False
    if delta == +8 and (pos % 64) >= 56: return False
    if delta == -64 and pos < 64: return False
    if delta == +64 and pos >= 448: return False
    return True

def slide_until_stop(pos, delta, maze):
    #若第一步就不合法,直接None
    if not can_step(pos, delta):
        return None
    cur = pos
    while True:
        nxt = cur + delta
        #保护
        if not in_bounds(nxt):
            return None
        #下一格是墙→停在当前格
        if maze[nxt] == 1:
            return cur
        #否则继续滑
        cur = nxt
        #下一步会越界(还没撞墙)→非法
        if not can_step(cur, delta):
            return None

def dfs(pos, goal, maze, visited, path, depth, max_depth):
    if pos == goal:
        return path
    if depth >= max_depth:
        return None
    visited.add(pos)
    for c, delta in MOVES.items():
        stop = slide_until_stop(pos, delta, maze)
        if stop is None or stop == pos:
            continue
        if stop not in visited:
            res = dfs(stop, goal, maze, visited, path + c, depth + 1, max_depth)
            if res is not None:
                return res
    return None

def solve(maze, start=0, goal=436, max_depth=30):
    return dfs(start, goal, maze, set(), "", 0, max_depth)

#用你的maze
goal = 436  #若题面是409则写409
path = solve(maze, start=0, goal=goal, max_depth=60)
print("solution:", path)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
from sys import setrecursionlimit
setrecursionlimit(10**6)

map1 = [0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00]
map2 = [0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00]


MOVES={'a':-1,'d':+1,'w':-8,'s':+8,'n':-64,'u':+64}

def inb(i): return 0<=i<512
def can_step(pos, d):
    nxt=pos+d
    if not inb(nxt): return False
    if d==-1 and pos%8==0: return False
    if d==+1 and pos%8==7: return False
    if d==-8 and (pos%64)<8: return False
    if d==+8 and (pos%64)>=56: return False
    if d==-64 and pos<64: return False
    if d==+64 and pos>=448: return False
    return True

def slide_until_stop(pos, d, maze):
    if not can_step(pos,d): return None
    cur=pos
    while True:
        nxt=cur+d
        if not inb(nxt): return None
        if maze[nxt]==1: return cur   #撞墙前一格停
        cur=nxt
        if not can_step(cur,d): return None

def dfs_dual(pos, goal, map1, map2, depth, max_depth, path, visited):
    if pos==goal: return path
    if depth>=max_depth: return None
    phase=depth&1
    maze = map1 if phase==0 else map2
    state=(pos,phase)
    if state in visited: return None
    visited.add(state)
    for c,d in MOVES.items():
        stop=slide_until_stop(pos,d,maze)
        if stop is None or stop==pos: continue
        res=dfs_dual(stop,goal,map1,map2,depth+1,max_depth,path+c,visited)
        if res is not None: return res
    return None

def solve_dual(map1,map2,start=0,goal=436,max_depth=60):
    return dfs_dual(start,goal,map1,map2,0,max_depth,"",set())

# 用法：
path = solve_dual(map1, map2, start=0, goal=436, max_depth=60)
print("solution:", path)

这个迷宫感觉不大对….